Lesson Modules
Teaching Tips:
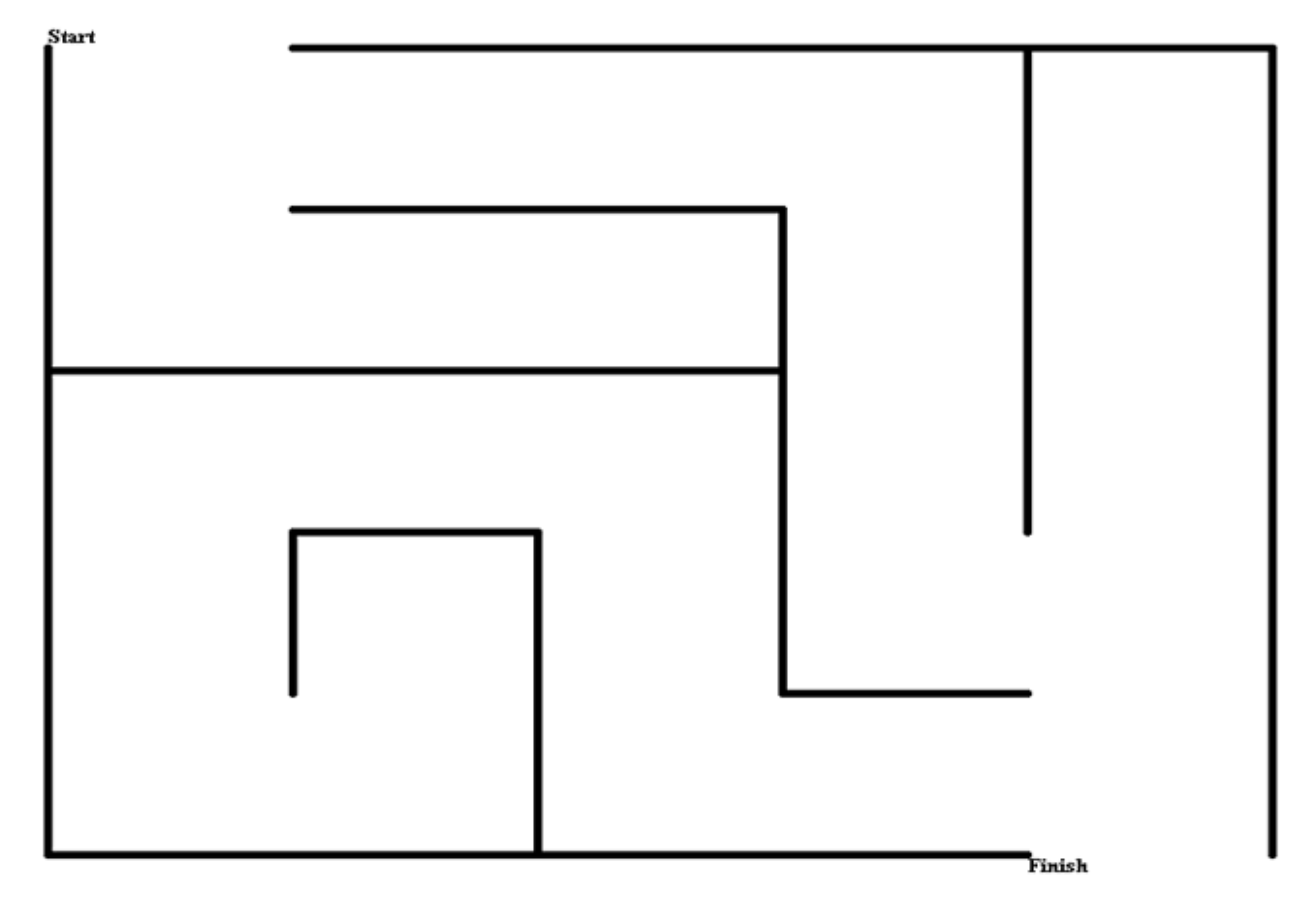
You probably recognise these from the coloring books of your childhood. It is a standard 2-dimensional maze.
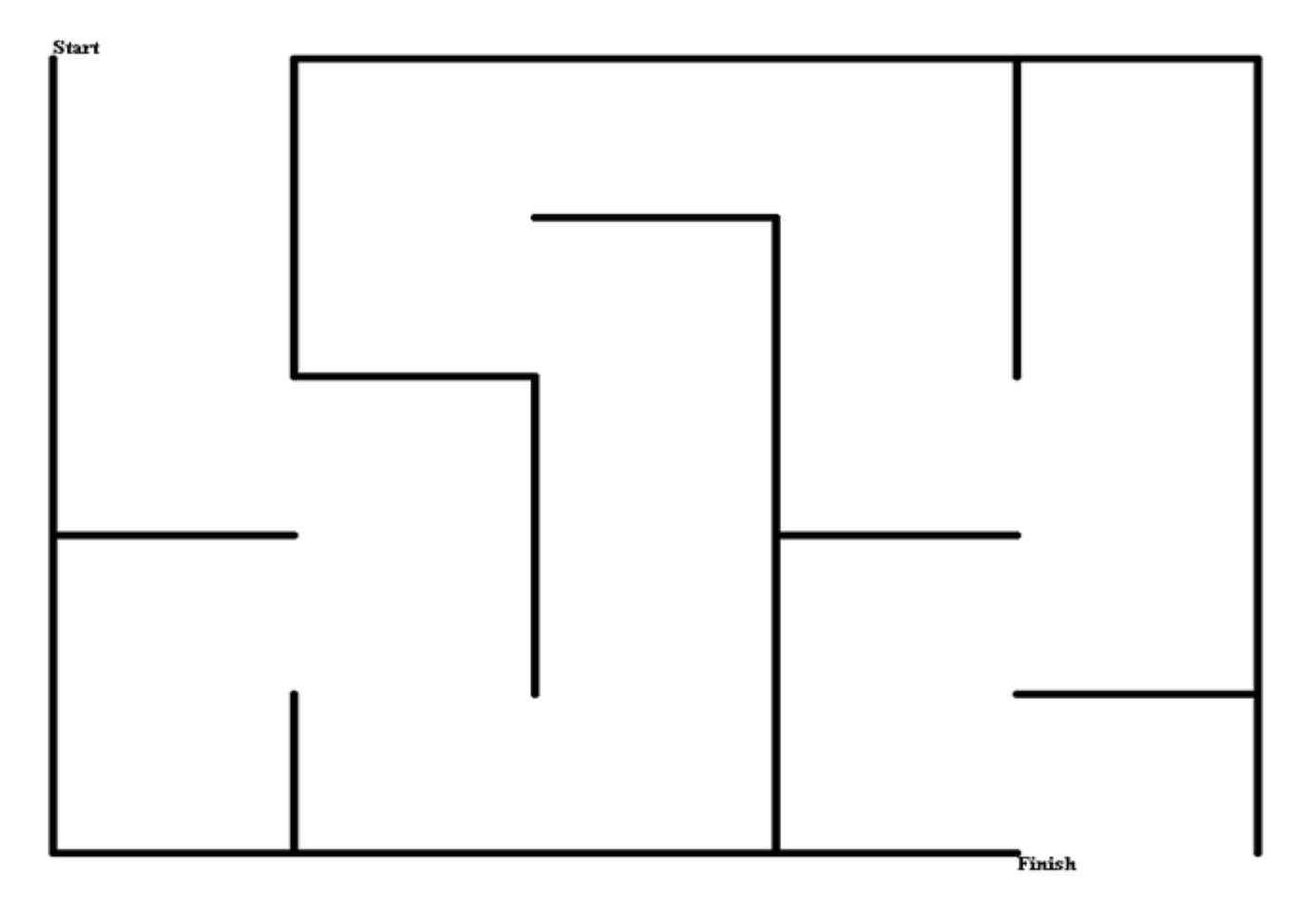
Try solving it for yourself.
How did you do that? Can you analyze a set of steps you took? Maybe you went down a path in your mind, and drew it in if you didn't see a dead end, maybe you just figured it out as you wrote it down, or maybe you did the whole thing in your head first! If you're like me, you can't pinpoint a specific strategy you used, you just solved it.
How might a computer solve this maze? If you said "using an algorithm" you'd be correct! Unlike a human being, a computer cannot take in the whole environment at once the way we can. It relies on the information it can sense right in front of it.
In the next section we weill look at some of the algorithms robots like the RobotLAB Autonomous car use to get through a maze.
Teaching Tips:
As you may have guessed, in this lesson we will build a maze and program the RobotLAB Autonomous car to solve it.
Here are some example mazes so you can get some ideas:
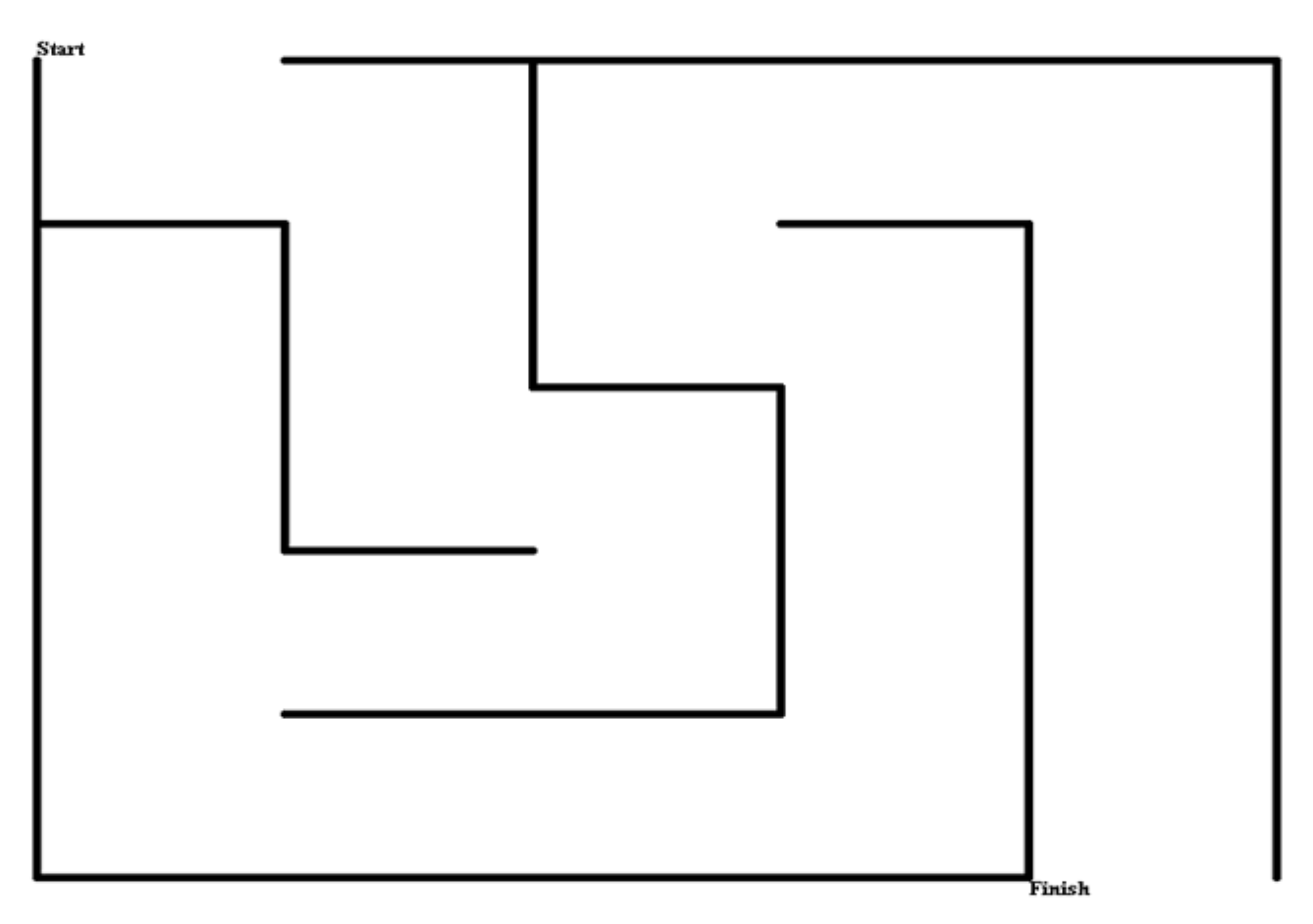
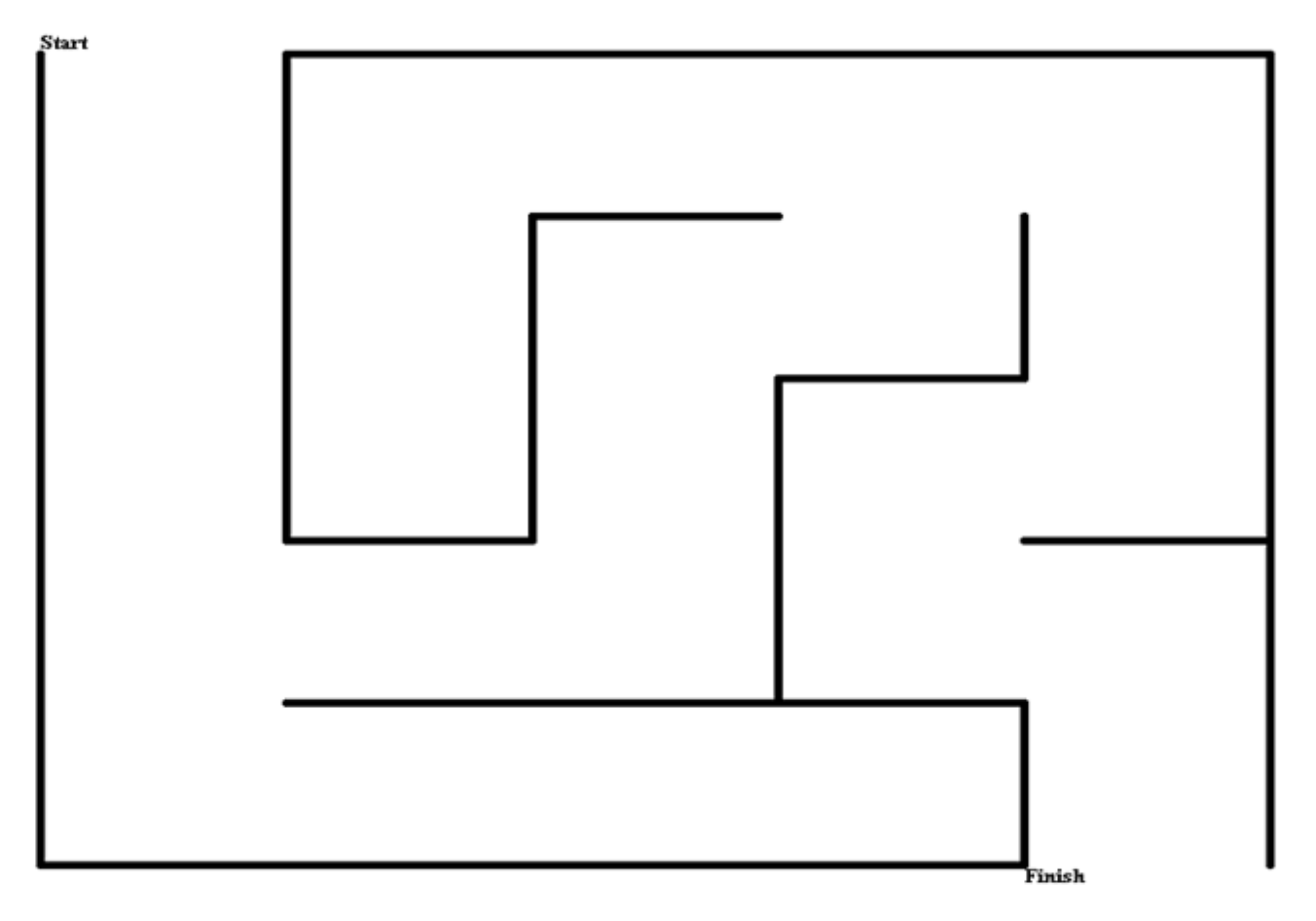
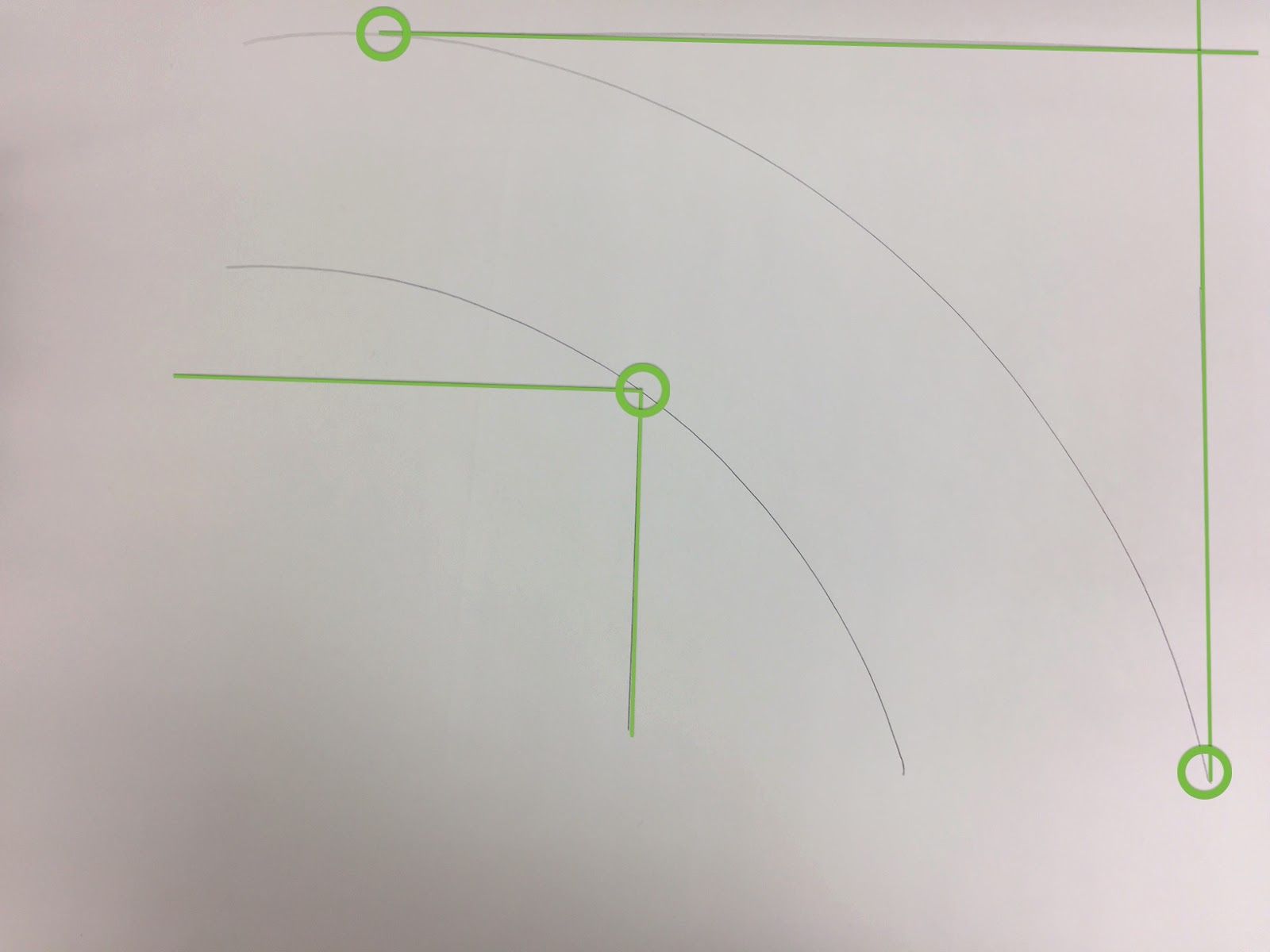
In order to create a usable maze for the RobotLAB Autonomous car, we need to know exactly how sharply it can turn. Take a large sheet of paper, and place the car on it. Make sure the car is turned off, then turn the front wheels to the left as far as they will comfortably go. Try pushing the car along with your hand. You will see the car turn as sharply as it can.
Hold a pen in your hand as you turn the car. Now you have captured how the car turns. Do the same on the other side. (For my measurement, I put the pen right behind the front wheel)



Your maze will probably be rectangular, so it will be easier to make your template with sharp edges. (This will also give the car a little leeway) An easy way to do that is to draw straight lines from the outer edges of the upper curve, and from the center of the inner curve.
The box your car came in is a good reference for how wide your path should be.

You may want to widen the part after the turn to match.

Finally, you can cut your template out and use it to draw a maze!

Remember to keep your maze simple.

Many maze solving algorithms exist for use with different robots in different situations. Here are four of the most common ones. (For this lesson, we can assume that all entrences and exits are on the outer walls of the mazes)
Random mouse
1. Go down a path.
2. When you reach a junction, pick a path at random and go that way.
This algorithm can take a very long time, but it requires very little memory. Theoretically, there are cases where this algorithm will never cease, and the mouse will never reach the end.
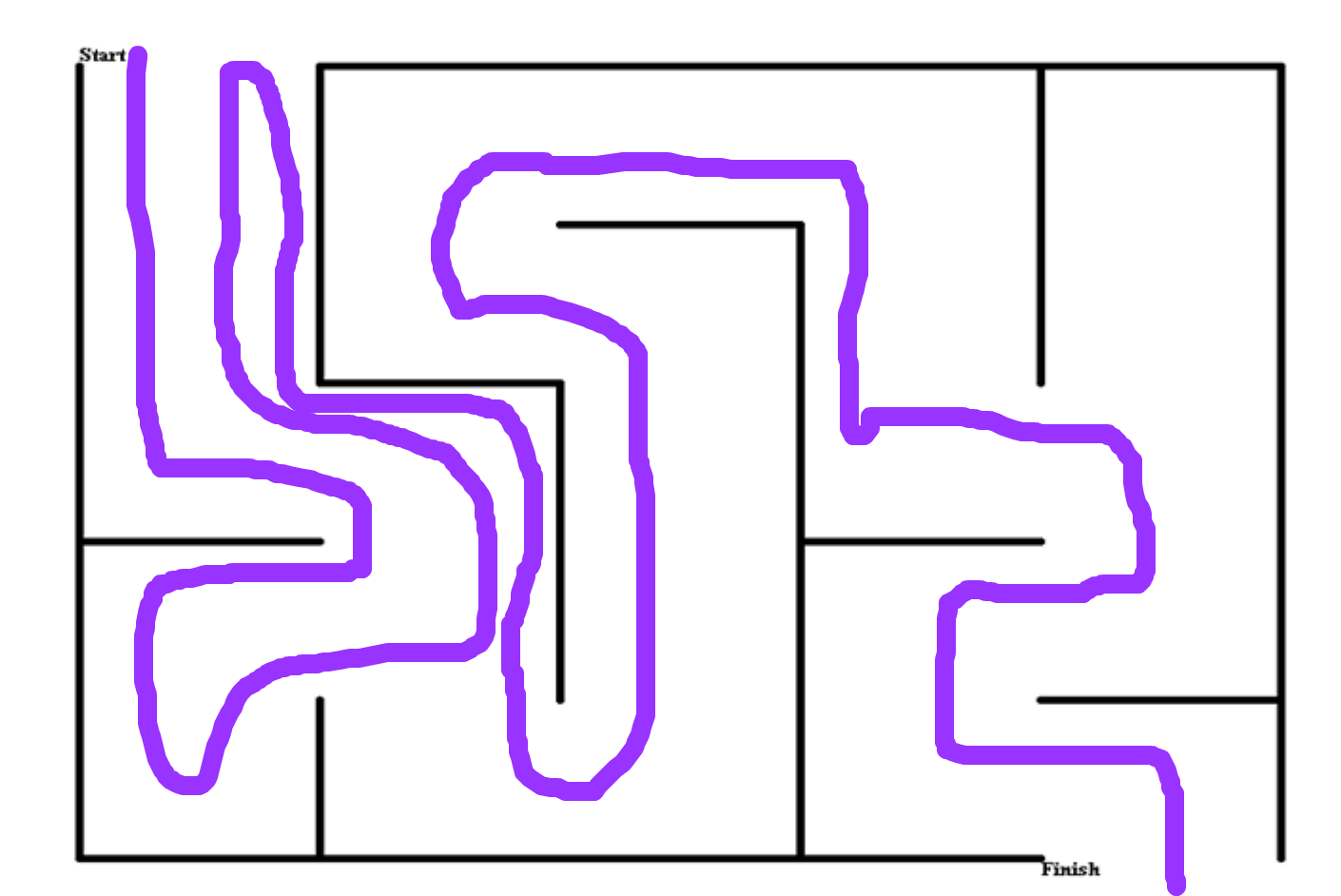
Wall follower (can be left or right-hand)
1. Choose a random starting direction.
2. At each intersection, take the rightmost turn. At dead-ends, turn around.
This algorithm will work faster than the random mouse, but it can get stuck!
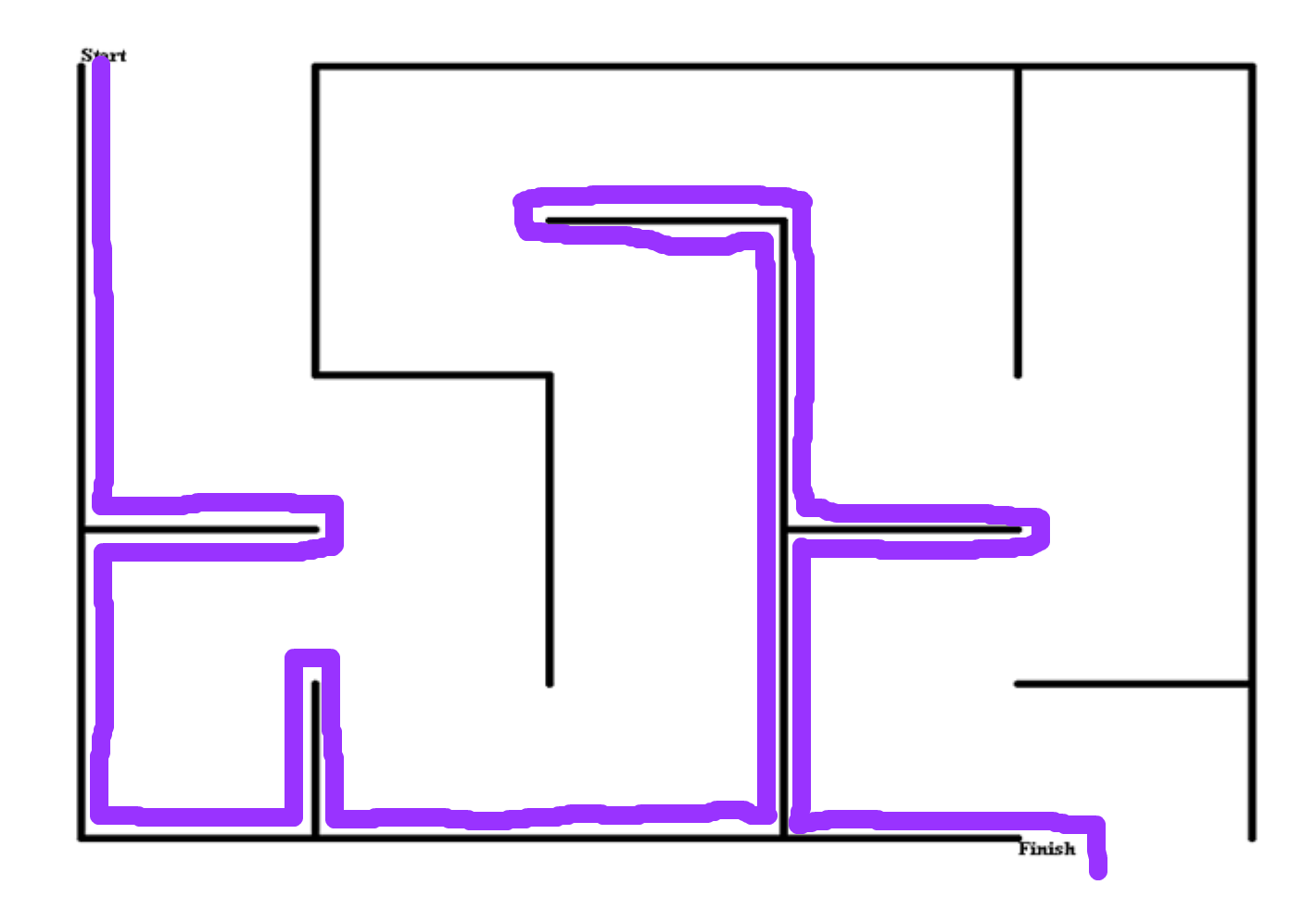
Pledge algorithm
1. pick a direction, and always move in that direction when possible.
2. When a wall is hit, start wall following until your chosen direction is available again.
When wall following, count the number of turns you make, e.g. a left turn is -1 and a right turn is 1. Only stop wall following and take your chosen direction when the total number of turns you've made is 0, i.e. if you've turned around 360 degrees or more, keep wall following until you untwist yourself.

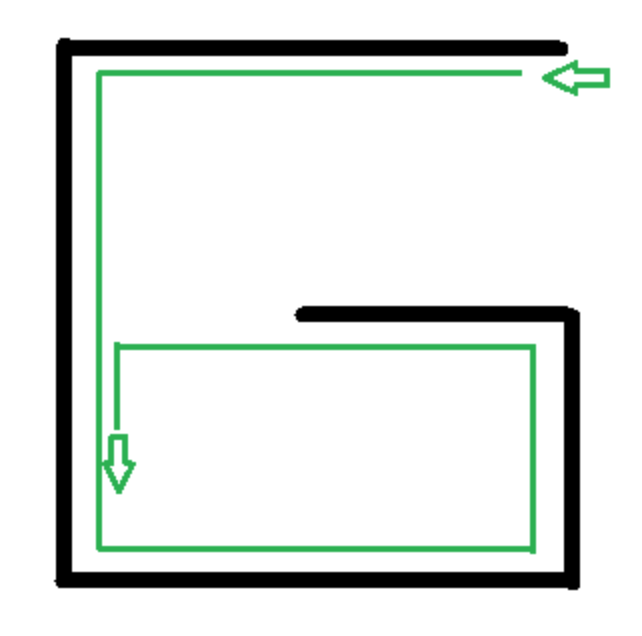
Tremaux’s algorithm
1. Pick a direction, draw a line behind you to mark your path.
2. When you encounter a junction you haven't visited before, pick a new passage at random.
3. When you hit a dead end, turn around and go back the way you came.
If you encounter a junction you have marked once, go back the way you came (marking your path a second time). If walking down a passage you have marked once and you encounter a junction, take any new passage if one is available, otherwise take one you've marked once. All passages will either be empty (haven't visited yet), marked once (gone down it exactly once), or marked twice, (gone down it and backtracked). Paths marked once will indicate a direct way back to the start.
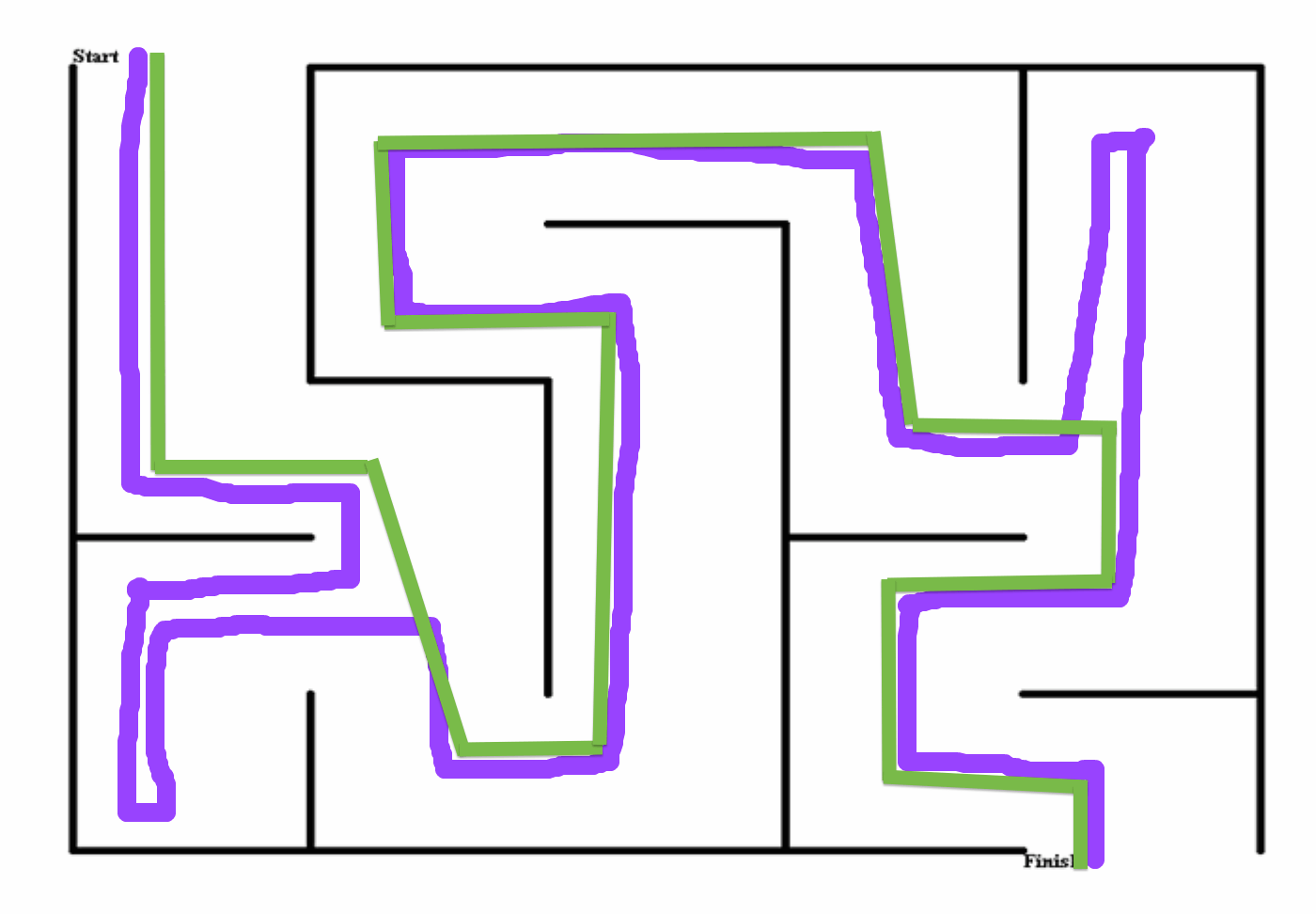
Teaching Tips:
In the last module you learned about 4 popular maze solving algorithms. They all have their merits, but which one is the best for our purposes? Take a look at the pseduocode again:
Random mouse
1. Go down a path.
2. When you reach a junction, pick a path at random and go that way.
What are the pros and cons of this algorithm?
PROS: very simple to execute
CONS: no guarantee it will solve the maze
Wall follower (can be left or right-hand)
1. Choose a random starting direction.
2. At each intersection, take the rightmost turn. At dead-ends, turn around.
What are the pros and cons of this algorithm?
PROS: pretty simple to execute
CONS: can get stuck
Pledge algorithm
1. pick a direction, and always move in that direction when possible.
2. When a wall is hit, start wall following until your chosen direction is available again.
What are the pros and cons of this algorithm?
PROS: won't get stuck
CONS: more complex
Tremaux’s algorithm
1. Pick a direction, draw a line behind you to mark your path.
2. When you encounter a junction you haven't visited before, pick a new passage at random.
3. When you hit a dead end, turn around and go back the way you came.
What are the pros and cons of this algorithm?
PROS: records the correct path
CONS: not possible with our robot
Which algorithm will you choose: Random Mouse, Wall Follower, Pledge Algorithm, Tremaux's Algorithm
I chose Wall Follower. Choose your algorithms and turn in your completed pseudocode.
Teaching Tips:
Here is the finished code:
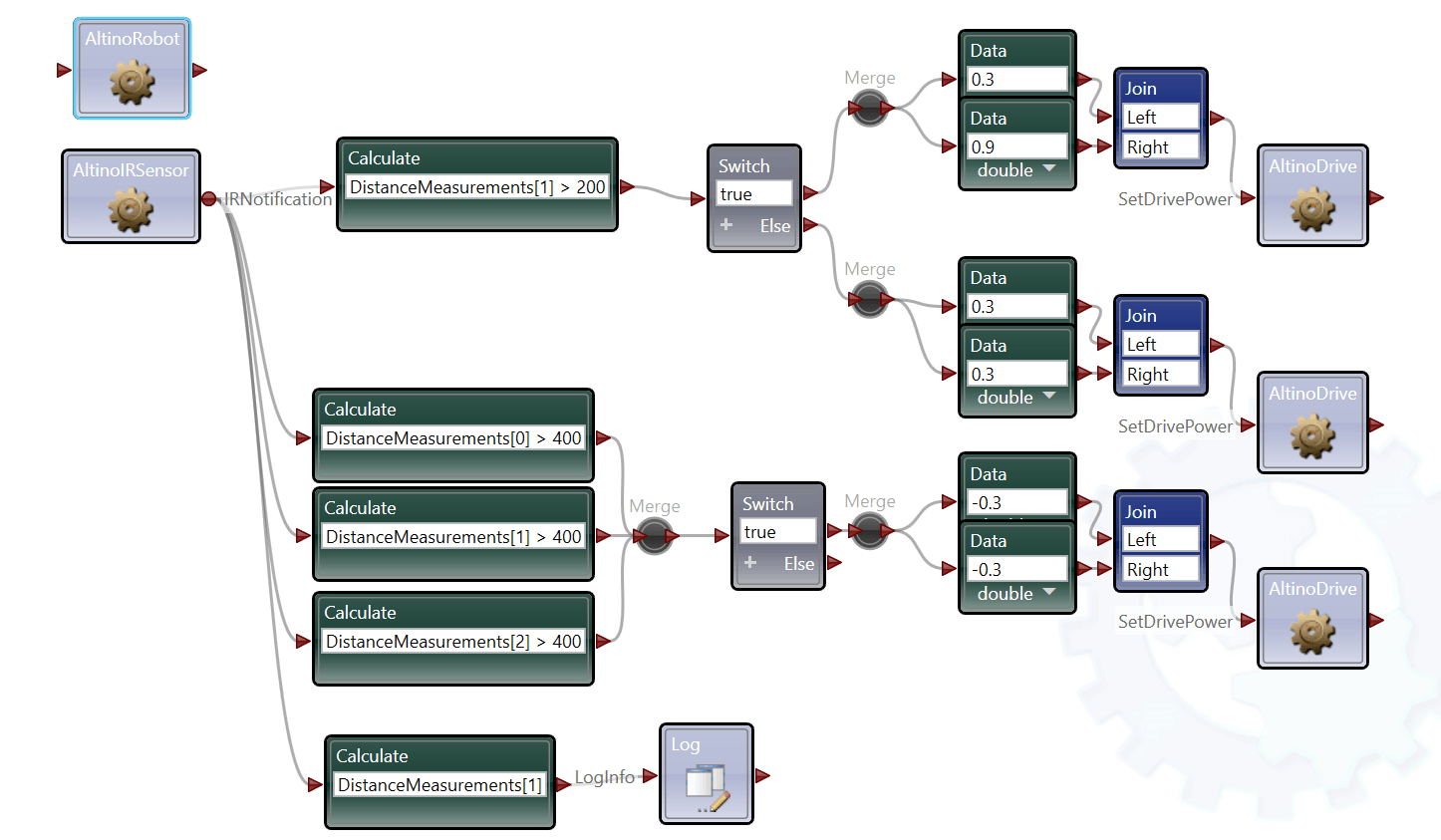
Here is the pseudocode for the wall follower:
1. Choose a random starting direction.
2. At each intersection, take the rightmost turn. At dead-ends, turn around.
Here is how I started my code:
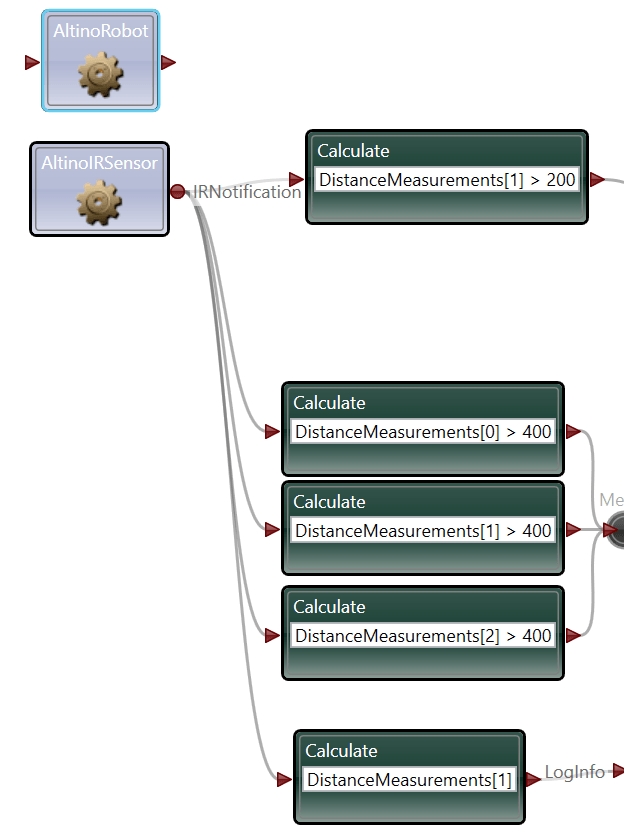
Remember, writing code is like writing a poem, there are many correct answers. Maybe you answered differently. If so, I encourage you to convert your pseudocode into code and see how it works!
Teaching Tips:
Question 1: Did your car solve the maze? If not, did it come close?
Any answer will do here. If time permits, have a short discussion with students about their answers.
Question 2: Check the concepts you understand. Don’t worry, this isn’t for a grade, it’s just so your teacher can check the classes’ understanding.
This is the students' self-assessment of their understanding of the material. You will see a bar graph once all the poll answers are submitted.
Question 3: Describe one of the maze solving algorithms?
Random mouse
1. Go down a path.
2. When you reach a junction, pick a path at random and go that way.
What are the pros and cons of this algorithm?
PROS: very simple to execute
CONS: no guarantee it will solve the maze
Wall follower (can be left or right-hand)
1. Choose a random starting direction.
2. At each intersection, take the rightmost turn. At dead-ends, turn around.
What are the pros and cons of this algorithm?
PROS: pretty simple to execute
CONS: can get stuck
Pledge algorithm
1. pick a direction, and always move in that direction when possible.
2. When a wall is hit, start wall following until your chosen direction is available again.
What are the pros and cons of this algorithm?
PROS: won't get stuck
CONS: more complex
Tremaux’s algorithm
1. Pick a direction, draw a line behind you to mark your path.
2. When you encounter a junction you haven't visited before, pick a new passage at random.
3. When you hit a dead end, turn around and go back the way you came.
What are the pros and cons of this algorithm?
PROS: records the correct path
CONS: not possible with our robot
- Wall-follower
- Random mouse
- Pledge