a1tD0000003mAqFIAU

Sine Graphs with Scratch

  • 9-12 grade

Lesson Description:

Students write an equation for the autonomous car to drive on a zig-zag road. This lesson helps amplitude, frequency, and vertical translation of graph of a sinusoidal function.


 

Standards Covered

CCSS.MATH.CONTENT.HSF.BF.A.1

Write a function that describes a relationship between two quantities.*

CCSS.MATH.CONTENT.HSF.IF.B.4

For a function that models a relationship between two quantities, interpret key features of graphs and tables in terms of the quantities, and sketch graphs showing key features given a verbal description of the relationship. Key features include: intercepts; intervals where the function is increasing, decreasing, positive, or negative; relative maximums and minimums; symmetries; end behavior; and periodicity.*

CCSS.MATH.CONTENT.HSF.TF.B.5

Choose trigonometric functions to model periodic phenomena with specified amplitude, frequency, and midline.*

CCSS.MATH.PRACTICE.MP1

Make sense of problems and persevere in solving them.

CCSS.MATH.PRACTICE.MP4

Model with mathematics.

CCSS.MATH.PRACTICE.MP5

Use appropriate tools strategically.

CCSS.MATH.PRACTICE.MP7

Look for and make use of structure.

image description

Lesson Modules


Teaching Tips:

A quick review of sine and cosine equations

Remind the students the sine and cosine equations as below.

{latex{\begin{align}y&=a \cdot sin(bx)+c\\y&=a \cdot cos(bx)+c\end{align}}latex}

where a is amplitude, b is frequency, and c is about horizontal shift.

 

Show the students the sine/cosine pattern (graph) on the road.

Note the grid on the surface that will help them make measurements.

Share the word cloud results with the student and have a quick discussion about the common answers. 

--> The students might say one road has a curvier and/or wider zigzag.

The learning concept of this lesson is 


1. amplitude
2. frequency
3. horizontal shift 

An autonomous car needs to drive on a curved road. Look at the two images to compare.

 

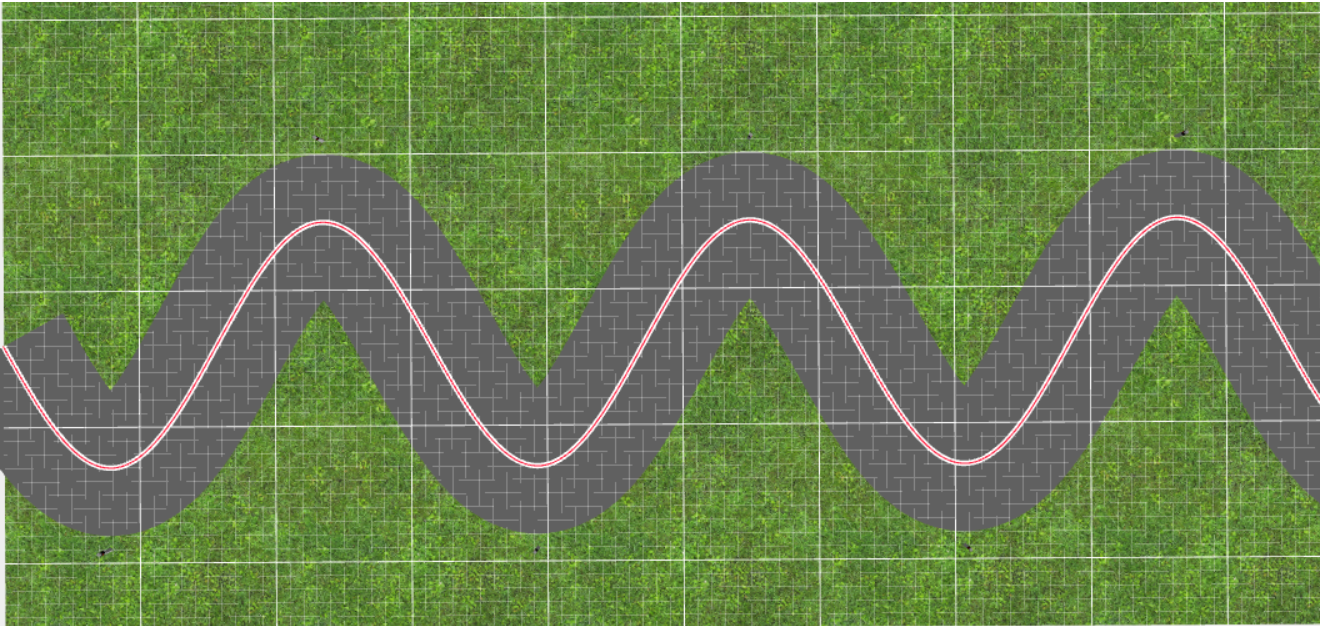What is the difference between the two roads above? Choose two factors. Type one factor for each question. You should answer using only ONE word.  


Type one factor that you notice the difference between the two roads. Type your answer using only ONE word.



Type another factor that you notice the difference between the two roads. Type your answer using only ONE word.

 


Teaching Tips:

Students can do this activity individually or in a small group. 

At the end of this module, have the students answer the questions. You have access to the students' input in the dashboard. 

You can use this time as a teaching moment or review time for the amplitude, frequency, and vertical/horizontal translations. 

Use the slide bars to adjust amplitude (a), frequency(b), and the vertical shift(c) to find the curve that the autonomous car can follow. 

For now, don't worry about formula or how to calculate the period & frequency. Just focus on the relationships between the a, b, and c variables and the amplitude, period, horizontal shift and look of the graph. 

Note: If you don't see the curve, click on the road and try to move a little bit.


What is amplitude? How does the amplitude in the equation change the graph? Type your answer in a sentence.
 

What is frequency? How does the frequency in the equation change the graph? Type your answer in a sentence.

 


Teaching Tips:

Guide the students to write and verify their equations on the simulation first. 

Before the students start programming Scratch, help them to think through the order of the statement. 

Print out this material for each group. 

Cut each item of blocks so the students can place them next to the statements.

Show the answer in the class view.

Have students program Scratch.

Have students run the autonomous car, observe how the car moves, and answer the questions. 

Simulation

Now that we understand how sine graph works, it's time to make our car drive on the road!

Note that you can generate new road patterns by clicking the Randomize button!

 

Direction: 

  1. See the curvy road and imagine where the car should move on. 
  2. What should the amplitude (a value) of the curve be?
  3. What should the period of the curve be?
  4. What is the frequency (b value) of the curve?

Hint: to calculate b value, use the formula {latexinline{ b=\frac{2 \pi}{period} }latexinline}.

  1. Use the amplitude and the frequency of the curve to write an equation. 
  2. Use the slides below for a, b, and c values to check your answer. 
 
A:
 

B:
 

C:
 

y=sin(x) +
  • Rotate View
  • Move Camera
  • Zoom In
 

 

 

 

Program the Autonomous Car

Print out this material. Cut each item of the blocks to match to the statement. 

Do not look at the answer before you try. 

Check the answer below and correct yourself.

A. Go with a certain power (speed) at a certain steering angle.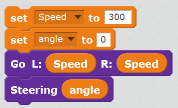
B. Continue for a certain interval time.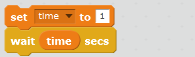
C. Go with the same power (speed) at a different steering angle.
D. Continue for the same interval time.
E. Repeat step C & D for a certain number of times.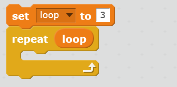

 

Now, open the Scratch from Orchestra program to try the blocks. If you don't have the Orchestra program on your computer, download it from here. 

Next, connect your autonomous car to your computer. Make sure you choose the right ID number of the device to avoid conflicts with another team.

1. Bluetooth2. Orchestra3. Scratch
 

Connect your autonomous car to your dedicated computer via Bluetooth.

Open Orchestra and connect your robot to the program.

Open Scratch from Orchestra

 

 

 

Run your code on the autonomous car. Did the car move as you expected? If not, discuss with your team members and fix your code as needed.

Observe how the car moves and answer the following questions. 



What is the amplitude of the curve on which the car moves?



What is the frequency of the curve on which the car moves?

What should you change on Scratch programming to make the car run with a bigger period of the curve?


Teaching Tips:

To avoid confusion, this lesson mentions only the frequency. If the students are ready, then introduce period vs. frequency. 

Check your knowledge on each concept.

I understand the concept of Sine and Cosine curves
  • Not at all
  • Not really
  • Kind of understood
  • Pretty much understood
  • Totally got it

Explain the similarity and the difference between sine and cosine graphs

I understand the concept of Amplitude
  • Not at all
  • Not really
  • Kind of understood
  • Pretty much understood
  • Totally got it

Explain how the bigger amplitude changes the graph.

I understand the concept of Frequency
  • Not at all
  • Not really
  • Kind of understood
  • Pretty much understood
  • Totally got it

Explain how the higher frequency changes the graph.

I understand the concept of Vertical Translate
  • Not at all
  • Not really
  • Kind of understood
  • Pretty much understood
  • Totally got it

What did you change in the equation to translate the graph vertically?