a1tD0000007kXvnIAE

Course: BOX V2
Slopes and Points Linear Functions

  • 6-12 grade
  • Intermediate

Lesson Description:

This lesson demonstrates the correlation of a linear function and coordinate points within the Cartesian coordinate system.  The student(s) are exposed to the concept of a point (x,y) and then challenged to use the demonstrated concepts to determine a corresponding formula based on given information such as two points or point and a slope.
Objective: Create a linear equation from two points or point and a slope.
 


 

Standards Covered

image description

Lesson Modules


Teaching Tips:

Make sure to download the Sphero Edu App in your phone before the class, and make sure students also count with the app in their groups. This app is compatible with all the new versions of Sphero, including the Star Wars versions.

Make sure to connect and aim the controller. You can create new programs with different functions. Once you press the start button, you will count with different graphs that can help students to analyze the slope and the different components of the function. This coordinate system is necessary to see the path that the robotic ball is moving along.

The first graph will always consider the starting point of the Sphero as the 0-coordinate. However, you can use Geogebra in order to analyze a function with different intercept values.

Next we need to make sure Sphero is charged and turned on.  To charge Sphero, you simply place it in the cupped charging receptacle.

It takes three hours to fully charge Sphero, but many times you can get through the lesson with less than a full charge.

Once Sphero is charged, you can shake the robot to turn it on.  The ball will briefly light up - signaling it is on.

When you have connected and positioned Sphero properly it is important to treat Sphero somewhat gently.  If you bump Sphero too hard or shake it too quickly it can throw off the internal calibration and the lesson must be restarted.

Lastly, we need to position Sphero in the proper orientation before beginning the lesson.  To do this, place Sphero in the proper location signified on the mat.

The initial rotation of the ball is also very important.  This orientation is used to internally calibrate the robot.

When you first connect to Sphero, a small blue dot will appear on the surface of the ball.  Align this dot with the arrow on the mat.

The mat can be used to a better understanding of the cartesian plane.

Sphero will now use its orientation as the initial calibrated position and from this point onward you are free to move the ball around as you wish. Sphero will maintain this calibration as long as you don't move the robot too rapidly.


Thinking about your last lessons, what would you need to know to define a line? Explain.


Teaching Tips:


The app allows us to quickly familiarize ourselves with the lesson to see how it operates.  By changing the values of the angle in the first block of the program, we can adjust the characteristics of the linear path that Sphero will move along. As we adjust the value of the slope in our code, we can see the path of the line change in the diagram. [insert picture here]

Sphero will move along the slope that you have entered, however if you change the intercept of the ball, you will need to physically re-position the ball prior to movement.

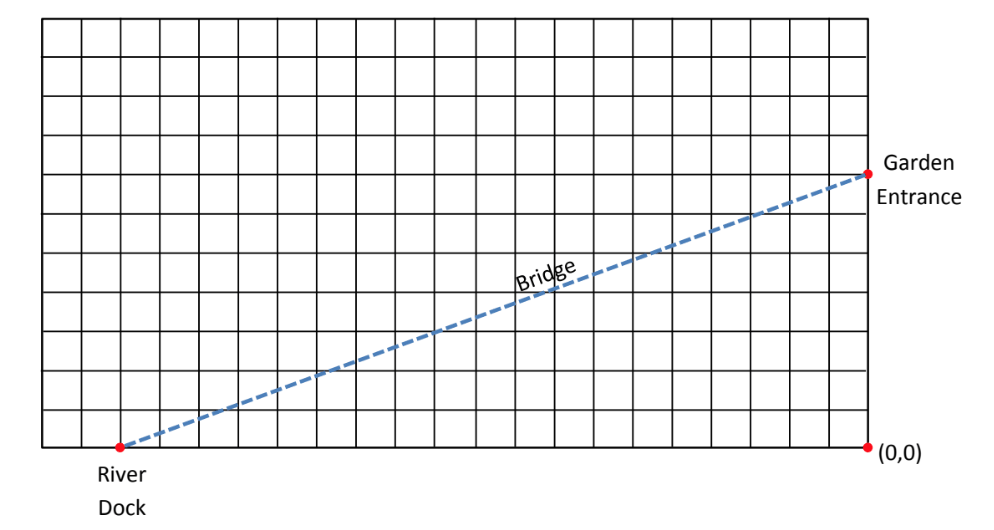
By moving Sphero along the mat you can determine the intercept. Sphero will move, and observe to see if the ball moves along the intended path.  For more intercept values, you may repeat this investigation as many times as you wish.


As we mentioned before, with the help of Geogebra, with the help of this platform you can easily display a graph of the path that you have chosen for Sphero to drive along. Note how this linear relationship is nearly identical to what is shown on the mat.

___________________________________________________________________________________

Go through Sphero with the students, explore the linear equation components, analyze the graphs and let students to explore the equation through the robot. Do not forget to respond their questions, and ask more to guide their curiosity.



Teaching Tips:

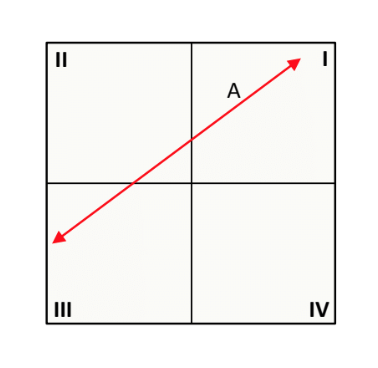
Think about how often linear paths and straight lines appear in your everyday life. List some of them (sidewalks, walking in a line, direct line of sight, etc.)

Choose the correct selection blow that illustrates line l with a positive slope:
  • A
  • B

Does line A have a positive or negative y-axis intercept?
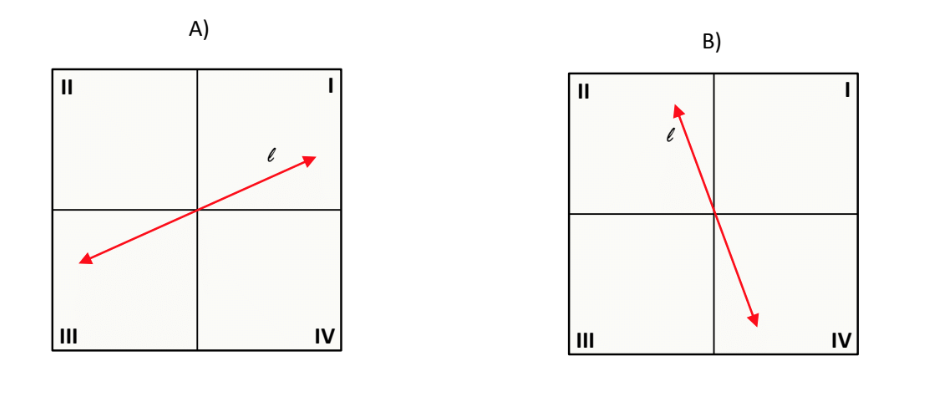
  • Positive
  • Negative

If a line has a negative slope, and its y-axis intercept is less than zero, what can you determine about where the function will cross the x-axis?

If a line has a y-intercept of 3, ΔX=10, and ΔY=5, what is the equation of the line?

If an engineer is looking to build a bridge from the garden entrance to the river dock, what is the slope that the bridge must take in the diagram below? The dock is 95 meters west of the origin, and the garden entrance is 35 meters north of the origin.

Considering that the fence is 10 feet tall and there is a bed of flowers that extends out 3 feet from the base of the fence, and that Bill wants to finish to leave when the shadow from the fence travels into the grass. What would be the equation of this?

The projector is mounted to the ceiling 10 feet off the ground. . The wall is 20 feet from the projector. The spot projected on the wall is 6 feet off the ground. What is the equation of the projected dot light beam’s path?

If the teacher decides to pull down the projection screen, which hangs two feet in front of the wall, how high above the floor will the dot be at point S?


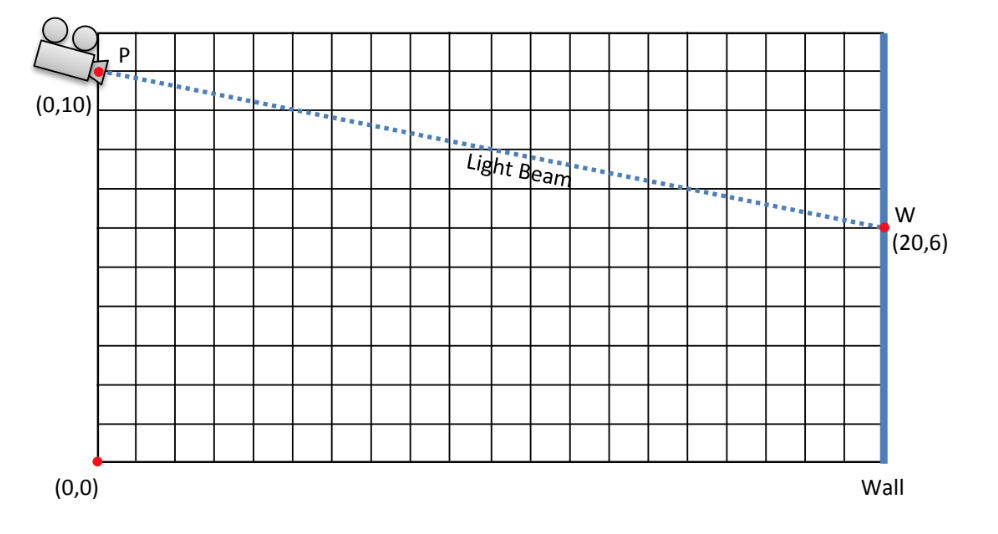
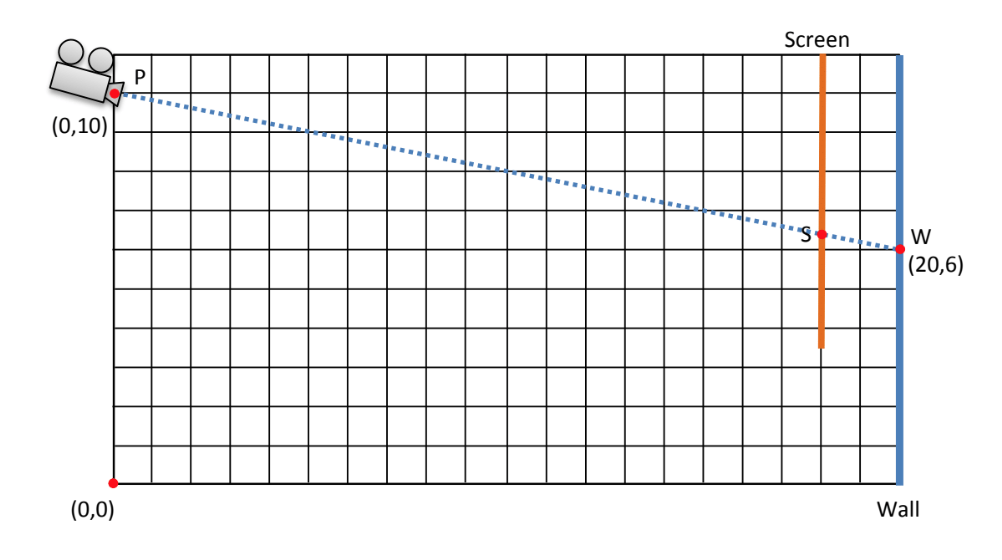
Teaching Tips:

Ask for volunteers to sketch their results on the board. Go through their answers, make sure they are correct, and finally, summarize the lesson.