a1tD0000003mAP2IAM

Course: High School Math with NAO
Slope of a Line with Two Points

  • 8-12 grade
  • Intermediate

Lesson Description:

Students determine the slope of a line that a soccer ball travels on so the NAO robot can score a goal. This lesson reinforces skills on the slope of a line with two points.


 

Standards Covered

CCSS.MATH.CONTENT.8.EE.B.6

Use similar triangles to explain why the slope m is the same between any two distinct points on a non-vertical line in the coordinate plane; derive the equation y = mx for a line through the origin and the equation y = mx + b for a line intercepting the vertical axis at b.

CCSS.MATH.CONTENT.HSA.CED.A.2

Create equations in two or more variables to represent relationships between quantities; graph equations on coordinate axes with labels and scales.

CCSS.MATH.CONTENT.HSF.IF.B.6

Calculate and interpret the average rate of change of a function (presented symbolically or as a table) over a specified interval. Estimate the rate of change from a graph.*

CCSS.MATH.PRACTICE.MP1

Make sense of problems and persevere in solving them.

CCSS.MATH.PRACTICE.MP2

Reason abstractly and quantitatively.

CCSS.MATH.PRACTICE.MP4

Model with mathematics.

CCSS.MATH.PRACTICE.MP5

Use appropriate tools strategically.

image description

Lesson Modules


Teaching Tips:

1) Explain the RoboCup robotic soccer competition to your students(//www.robocup.org/objective).

2) Show the video in the Class View section.

3) Have students type their ideas

4) Share the results in the word cloud (class view).

5) Discuss the results. 

 

Have you ever played soccer? There are many soccer players and fans all over the world, including the NAO robot. NAO is an amazing soccer player as you will see today. 

Have you ever heard of the Robot Soccer World Cup (RoboCup)? It is an annual international robotics competition. Your teacher will show a video of the RoboCup match today. 






What does the robot need to know in order to score a goal? Type your answer using only ONE word.


Teaching Tips:

Encourage students to work in small groups and visualize the key information needed to solve this challenge. 

The interactive tool helps students visualize the mathematical figures in the soccer scenario. 

Challenge:

Imagine you are the coach of the NAO soccer team. You must give the right instructions to make as many goals as possible. A goal is scored when the whole ball passes over the goal line, between the goalposts, and under the crossbar. See the animation below to become familiar with the soccer field.

Your NAO robot will attempt a goal. Your job is to give NAO the equation that leads it to the right place to kick the ball and score a goal. Use the information below to figure out the equation and answer the following question. 

Visualize the line that the ball travels on for NAO to score a goal. 


User-added image

 

Directions: Follow the directions below. 

  1. Imagine where you want the ball to go.
  2. Click on the empty box next to Goal Line.
  3. Move the slope slider to match the kicking line you want the ball to travel on.
  4. Place a point where the goal line and the kicking line meet. 
  5. Calculate the slope of that line. 

 

 



What do you estimate of the slope of the line to be? Type your answer using only the number.



Teaching Tips:

Show the class how to use the simulation. 

Have students run the simulation individually or in a small group. 

Have students take turns connecting NAO robot to test their answer (utilize the robotmaster protocol). The groups can compete as if they were playing a game. At the end of the game, you can give an award to the winning team. 

Simulation 

Use the simulation below to practice your skills. 

Find the slope of the line on which the ball should travel in an attempt to score the goal for NAO! Type the slope in the equation. The equation is written in the point-slope form.

  • You can see the grid-in lines by clicking Show Grid. 
  • You can zoom in and out.
  • The randomize button will change the ball position. 
  • When you are ready, click on Run Simulation button to check if your slope will score a goal. 


  
    

Show Grid
Equation: y =
  • Rotate View
  • Move Camera
  • Zoom In

The field is a rectangle of width 1.4 meters and a length of 2 meters.

The goal line is 50cm wide and the center of the table is at position (0, 0).


The ball has been randomly placed on the table at position (23,27), which gives the above equation for a line going along the field through the ball.

The value of the slope has been left blank in the above equation - enter an estimate and hit "simulate" to see if NAO player scores a goal!



Run the real robot!



When you are ready - it's time to run it on the real robot!

Place NAO robot before the ball, facing the goal line. The distance between the robot and the ball should be 20 centimeters. 



Open this Choregraphe file.

You will see this interface once you open the file.

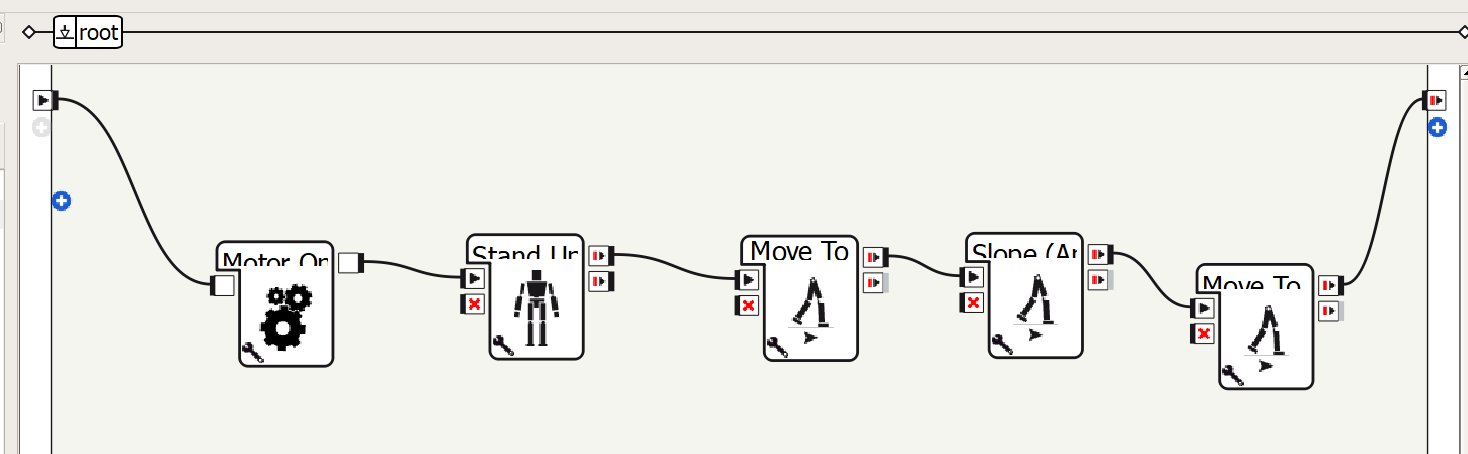
Click on the wench of the Slope box. You will be able to change the parameters.

Change the Theta (deg) value based on the converted slope. 

Click OK button. 

Run the program on NAO by clicking on the green play button on the left top corner.


Teaching Tips:

Have students individually reflect on what they learned today. You can access the qualitative answers and the data in the teacher dashboard.

If time is allowed, have a quick discussion about what went well and what could have been done differently in order to facilitate learning.

Students' responses to the questions will appear in the Class View as Bar graphs or pie charts, you can use these to aid your discussion with the class. 

At this point of the lesson, you should be able to recognize the slope of a line as a number that measures "steepness ". You should also recognize that it is the change in y for a unit change in x along the line. You should be able to calculate the slope by using the rise-over-run formula. 

Reflect on what you've learned by responding to the questions below.  Don't worry, your response won't be graded. It will give you a chance to reflect on your learning and for your teacher to see your responses.

 

I understand this concept: Slope as a number that measures its steepness
  • Not at all
  • Not really
  • Kind of understood
  • Pretty much understood
  • Totally got it

 

Explain what a slope of a line tells you about the line.

 

I understand this concept: Rise-over-run method
  • Not at all
  • Not really
  • Kind of understood
  • Pretty much understood
  • Totally got it

 

Explain how you calculate the slope of a line


Teaching Tips:

Questions to Ponder

Ask the following questions to deepen students' knowledge. Encourage students’ creativity. There is more than one way to do this task. Students keep using the same scenario of the soccer field. 

You can ask questions below:

  • What does it mean by "having the same kicking line"?
  • Can the ball move and still have the same kicking line?
  • Can we have the same slope even if the ball is in a different position?
  • Why are there many sets of points that still create the same line?

NAO player will follow the kicking line to attempt a goal. Where else can you place the ball and still have the same kicking line? See the picture below.

TIP: SLOPE IS A RATIO!