Lesson Modules
Teaching Tips:
Once you open the lesson, you will be presented with a series of items that will need to be completed before you continue onward to the lesson.
The first step is to position the tablet and mat properly. The Mat has three brightly colored shapes that must be matched up with colored silhouettes found on the tablet screen once the lesson has begun. The Tablet should be clipped into the Mount included in your BOX, with the screen facing up and the camera on the back of the Tablet facing down toward the Mat. Clamp the Mount to your BOX or a nearby table – somewhere solid and secure.
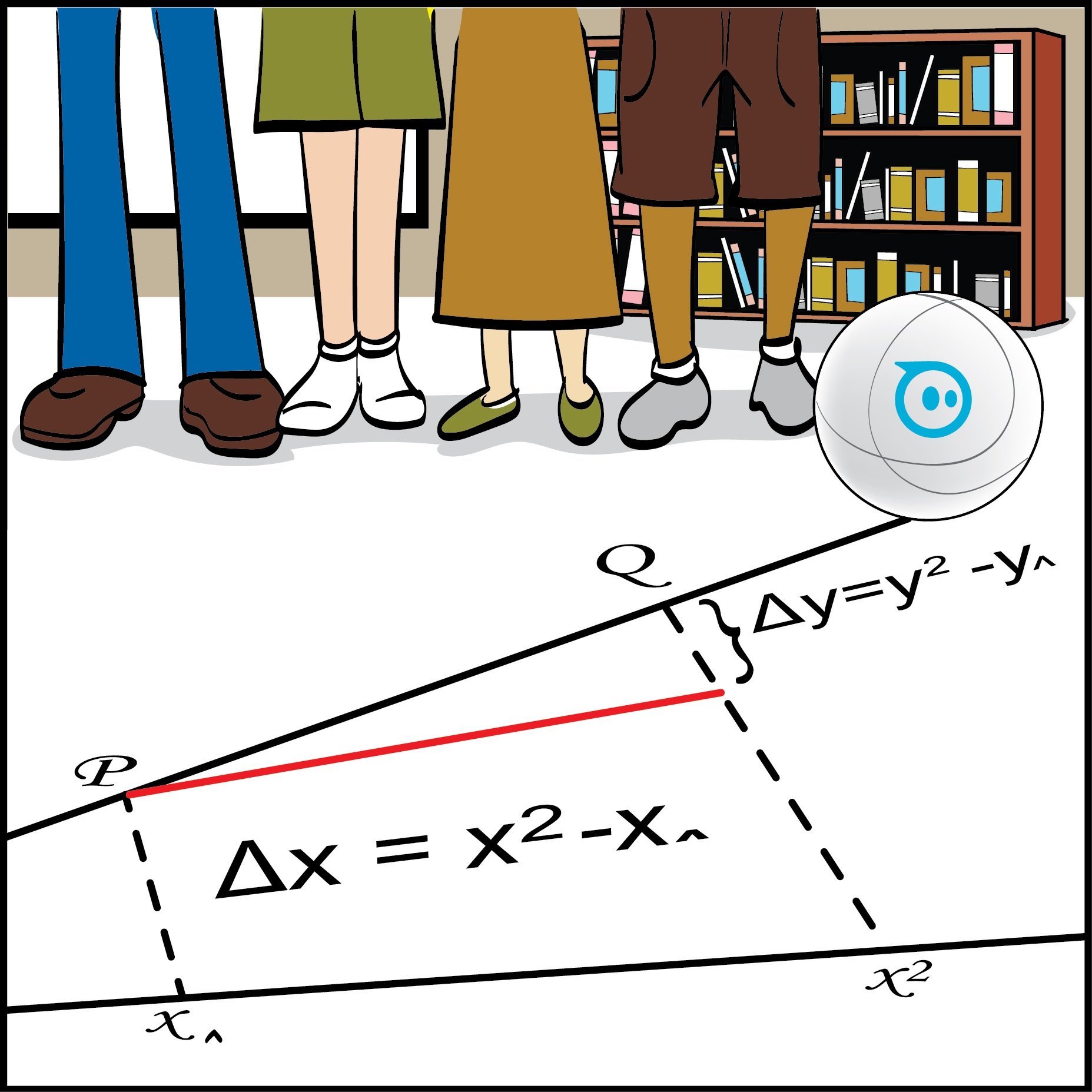
This lesson takes the square, circle, and triangle and generates an augmented reality coordinate system that fits within the area of the mat.
This coordinate system is necessary to see the path that the robotic ball is moving along.
Next we need to make sure Sphero is charged and turned on. To charge Sphero, you simply place it in the cupped charging recepticle.
It takes three hours to fully charge Sphero, but many times you can get through the lesson with less than a full charge.
Once Sphero is charged, you can shake the robot to turn it on. The ball will briefly light up - signaling it is on.
When you have connected and positioned Sphero properly it is important to treat Sphero somewhat gently. If you bump Sphero too hard or shake it too quickly it can throw off the internal calibration, and the lesson must be restarted.
Lastly, we need to position Sphero in the proper orientation before beginning the lesson. To do this, place Sphero at the bottom left of the frame on the mat with dot facing towards the positive X.
The initial rotation of the ball is also very important. This orientation is used to internally calibrate the robot.
When you first connect to Sphero, a small blue dot will appear on the surface of the ball. Align this dot with the positive direction of the x-axis.
The ball should be placed on the mat as illustrated in the image below. Note the location of the arrow and blue dot.
Once you have continued through the selections successfully and Sphero is positioned properly, press the green start button to begin the lesson.
Sphero will now use its orientation as the initial calibrated position and from this point onward you are free to move the ball around as you wish. Sphero will maintain this calibration as long as you don't move the robot too rapidly.
Teaching Tips:
Now that the lesson has started, you need to adjust the position of the tablet (height and angle) until the colored shapes on the Mat appear inside their matching silhouettes on the tablet image. Once all the shapes are shown inside their silhouettes, clamp the tablet into its final position. The tablet grid is now calibrated and you can move on with the lesson.
In this first screen, we have a column on the left along with an image of the working mat in the center, and positional data on the far right. The data on the right displays information about where Sphero should be placed. In this initial screen, Sphero should already be resting at the origin.
Going back to the gray column on the left - at the top displayed in bold, we have the equation of the path of the line that is displayed on the graph.
Directly, below are three tabs: Prepare, Demonstrate, and Investigate.
The Prepare tab (which is the default mode that the lesson starts in), allows us to quickly familiarize ourselves with the lesson to see how it operates. By pushing on the vertical bars in the left column, we can adjust the characteristics of the linear path that Sphero will move about.
The area on the left allows the user to change the slope of the line (m), its angle, as well as the change in X and Y values. All slide bars affect the factor m in the formula y = m(x)+b.
As we adjust the value of each slide-bar, we can see the path of the line change in the diagram.
Keep in mind that in this ''preparation'' mode, Sphero does not actually move. This is just a virtual mode to illustrate how the lesson operates.
Additionally, there is an orange tab called ''GRAPH'' located to the immediate right of the gray column.
You can drag or click this tab to display a graph of the path that you have chosen for Sphero to drive along. You can switch back and forth between the two displays. Note how this linear relationship is nearly identical to what is shown on the mat.
Once you are comfortable with how the lesson operates, we are ready to move onward with Sphero movement. To begin, click the ''demonstration'' tab. In demonstration mode, the screen appears almost identical to that of the ''prepare'' tab except that we now have the addition of a large green button in the lower-right corner of the screen. This button initiates Sphero movement. Initially, it appears green signifying that Sphero is ready to move. When pressed this button will turn red, and Sphero will move along the path chosen by the slide bars.
Again, in the demonstration mode, you can pull out the ''GRAPH'' tab to display the linear path of Sphero.
Once Sphero has completed its movement, the button will turn green again, and you may re-position the ball back on the mat and run again. This can be done as many times as you wish.
The next tab titled ''Investigate'' challenges the students to guide Sphero along the proper path. Presented on the right in orange lettering is a question that the students are challenged to complete.
When an answer is determined, adjust the value of the slope in the entry wheel and press the green play button to move Sphero.
For more challenges, hit the ''shuffle'' button on the left to formulate a new challenge. You may repeat this investigation as many times as you wish.
When you are done with the lesson, press the blue back button in the upper-right corner of the screen. This will return you to the lessons selection menu.
____________________________________________________________________________
Go through Sphero with the students, explore the slope of linear equations, analyze the graphs and let students to explore the equation through the robot. Do not forget to respond their questions, and ask more to guide their curiosity.
Teaching Tips:
Quiz Answers- Slope Based Linear Guidance (Positive Numbers) Answers
- The slope of a line is related to the rise over the run in a graph. The slope of a line is also related to the angle formed between two lines as the tangent of the angle equals to the rise over the run. We use this demonstration to make visual sense of the meaning of the slope of a line.
- Given the angle, just find the tangent of that angle. Given two points, find the change in y coordinates over the change in the x coordinates (rise over run).
- B
- B
- C
- D
- A
- 7
- 2
- 4
- 5
- 10
- 0
- 20
- Undefined
- 4
- 2
- 1
- 3
- 4
- 2
- 1
- Undefined
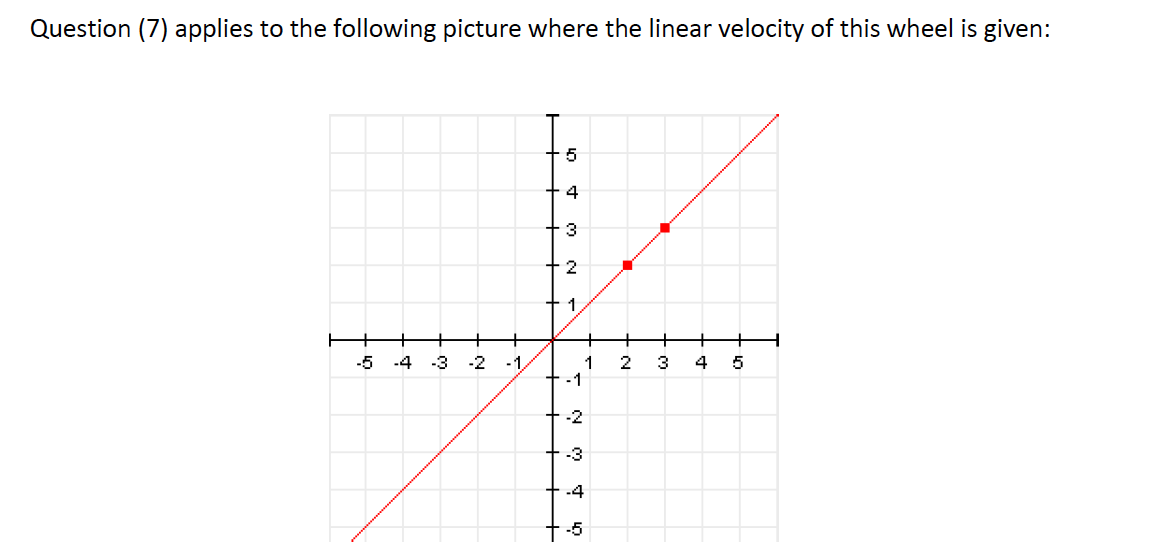
- 1
- 6
- 44
- 0
Teaching Tips:
Ask for volunteers to sketch their results on the board. Ask for a student to summarize these on the boards for students to write down.