a1tD0000003mD5aIAE

Course: Motion and Math
3: Raise the Roof

  • 6-8 grade
  • Intermediate

Lesson Description:

In this lesson, the students will 1) move the robot’s arms in unison, and 2) transition the robot from one action to another.  


 

Standards Covered

CCSS.MATH.CONTENT.6.NS.C.5

Understand that positive and negative numbers are used together to describe quantities having opposite directions or values (e.g., temperature above/below zero, elevation above/below sea level, credits/debits, positive/negative electric charge); use positive and negative numbers to represent quantities in real-world contexts, explaining the meaning of 0 in each situation.

CCSS.MATH.CONTENT.6.NS.C.6

Understand a rational number as a point on the number line. Extend number line diagrams and coordinate axes familiar from previous grades to represent points on the line and in the plane with negative number coordinates.

CCSS.MATH.CONTENT.6.NS.C.8

Solve real-world and mathematical problems by graphing points in all four quadrants of the coordinate plane. Include use of coordinates and absolute value to find distances between points with the same first coordinate or the same second coordinate.

CCSS.MATH.CONTENT.6.RP.A.1

Understand the concept of a ratio and use ratio language to describe a ratio relationship between two quantities. For example, "The ratio of wings to beaks in the bird house at the zoo was 2:1, because for every 2 wings there was 1 beak." "For every vote candidate A received, candidate C received nearly three votes."

CCSS.MATH.CONTENT.6.RP.A.3

Use ratio and rate reasoning to solve real-world and mathematical problems, e.g., by reasoning about tables of equivalent ratios, tape diagrams, double number line diagrams, or equations.

CCSS.MATH.CONTENT.7.RP.A.1

Compute unit rates associated with ratios of fractions, including ratios of lengths, areas and other quantities measured in like or different units. For example, if a person walks 1/2 mile in each 1/4 hour, compute the unit rate as the complex fraction 1/2/1/4 miles per hour, equivalently 2 miles per hour.

CCSS.MATH.PRACTICE.MP1

Make sense of problems and persevere in solving them.

CCSS.MATH.PRACTICE.MP2

Reason abstractly and quantitatively.

CCSS.MATH.PRACTICE.MP3

Construct viable arguments and critique the reasoning of others.

CCSS.MATH.PRACTICE.MP4

Model with mathematics.

image description

Lesson Modules


Teaching Tips:

RAISE THE ROOF


Problem of the Day:

"How can I make NAO move his arms to music in unison?"

Vocab:

  • Mirroring

 

Students will be able to...

Make the robot’s arms move in unison and transition it from one action to another.

 

Content

Students will continue to familiarize themselves with negative numbers. In addition, they will experiment with symmetry and mirror.

 

Learning Overview:

  1. Intro: Students will follow NAO in a dance
  2. Problem Solving: Students will explore how to control the arm motors and use the mirroring feature. 
  3. Creative Time: - Students will use these skills to create their own arm movements
  4. Reflection: The class will discuss what they learned and show off their creations

 

Before the Lesson:

Download the Choregraphe files onto your computer

For the intro dance activity, load lesson3_1 choregraphe file onto one of the robots. Leave at least 2 feet on all sides to do his dance. Clear an area for students to gather and watch the NAO. They will be mirroring NAO’s movements, so be sure to leave enough space for them to move! Read the reference sheet for this lesson.


 

LESSON INTRO


The students should stand arms-distance apart. Play the lesson3_1 choregraphe file and have the students mirror NAO’s movements.

If you don't have a NAO robot, use this video in class view so the students can mirror the dance. 

 

 
 

BEFORE THE CLASS

Before you begin, wash your hands. This should be a daily routine because the robots are white and get dirty easily.



OBSERVATION

 
Make sure you have plenty of space around you and mirror NAO's dance. Enjoy!
 
 



Let’s say that you are a choreographer who designs the dance. What would you need to know to make NAO dance? Type your answer in only one word.



Teaching Tips:

 

PROBLEM SOLVING


Student Discovery (5 minutes)

Pose the problem of the day to the students. Then have them fill out the “Make a Plan” section of their student book. This is a complex problem so make sure your students break it down into smaller parts. They need to know how to

  1. Control the arm angles 
  2. Save arm positions in keyframes
  3. Make the arms mirror each other

 

They should do this breakdown independently, with prompting as needed from you and your assistants. Do not worry about how good the breakdown is. 


Note: For the Question 3, the students’ answers must be only one word. If there is a space in their answer, the system won't read the answer properly. For example, if the answer is "Animated Say", students should type "AnimatedSay" or "Animated_Say". 

 

Teacher Talk Time (5 minutes)

Walk the students through all the motors in the robot’s arm. Specifically, show them the two rotational directions of the shoulder and elbow. Demonstrate the mirroring feature and the difference between the arms when starting in identical positions vs. different positions. Explain that mirroring is like having a mirror down the center of your body. What one arm does, the other must also do. Additionally, demonstrate how to change perspective in Robot View. Details can be found in the reference sheet. 

 

Solve the Problem (10 minutes)

Have the students work individually on the “Simon Says!” activity. This activity’s purpose is for students to get a feel for how the arm motors work. The students must mimic the picture and record the angles of each motor.



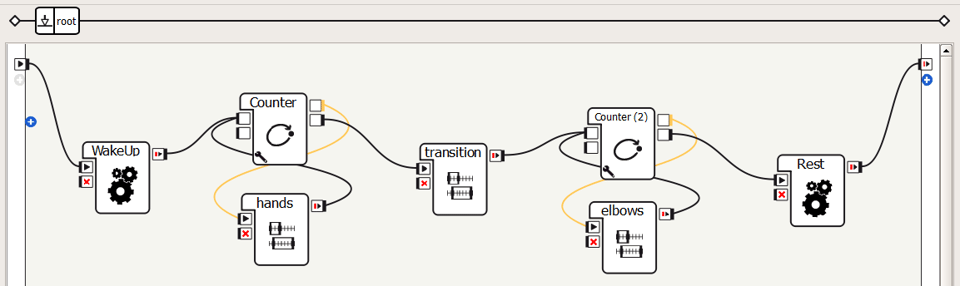
Example Program for transitioning between looped motions.

 

 

MAKE A PLAN

 
"I want NAO to move his arms together!"

 
Answer the following questions.
 
What do you already know about programming the robot that could help you solve this problem? 
 
What do you need to learn to solve this problem?
 
 
Draw a picture
Draw a picture of what you want NAO to do. 

 
 

Look for Choregraphe Boxes that might be helpful in solving this problem.
 


Which box do you think is helpful in solving the problem? Write in one word.




SIMON SAYS


Click on the virtual NAO’s arms to change the positions. Try to match your virtual NAO to the pictures below. Fill in the motor angle measures, rounding to the nearest integer (whole number). 


 


When you look at NAO, his right arm is on your left and his left arm is on your right. Explain why.




 

 



Teaching Tips:

CREATIVE TIME


Teacher Talk Time (5 minutes)

Show the students what happens if you don’t include a transition box. See the lesson3_2 Choregraphe file for an example. Encourage students to come up with two motions for the arms and transition between them. 

 

Plan (10 minutes)

Have the students fill out the “Your Dance!” section to plan out their dance moves.

 

Implement (15 minutes) 

Students will work on programming their planned movements. They must test their motion on the virtual robot before they are allowed to test it on the real robot. Be sure to sketch the program. 
 

YOUR DANCE

 

Find the angles of the arm joints that will make the robot "raise the roof".

Plan your arm actions by drawing keyframes in the squares below. Remember that when you put the keyframes in timeline, you will have to make the first frame and last frame identical.


Action 1:


Transition:



Action 2:

 

HAVE NAO DANCE!!

When you are ready - it's time to run it on the real robot!

Open Choregraphe. Ask the teacher before connecting and running the real robot. 

NAO has six motors in each arm. They are called,

  1. Shoulder Roll
  2. Shoulder Pitch
  3. Elbow Roll
  4. Elbow Yaw
  5. Wrist Yaw
  6. Hand

The terms yaw, roll and pitch refer to the orientation of the axis of rotation of each motor. Refer to the diagram on the right or below.



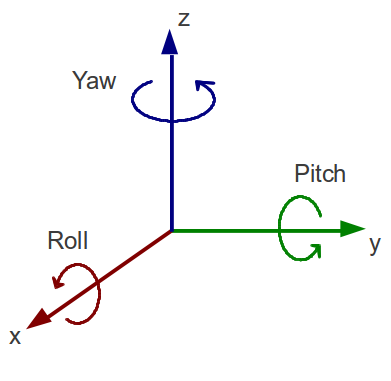
When you click on the arms you might notice that the right and left arms control boxes are mirror images. Additionally, some angle measures are negative of one another. This is because angles are commonly measured so that counterclockwise is the positive direction and clockwise is negative. Play around with the angles to get a feel for the different motions NAO can do.


Teaching Tips:

Reflection (10 minutes)

Have the students fill out the “Reflect” activity. Give them 2 minutes to journal silently. Then have them volunteer their responses to help stem a discussion.

After the Lesson:

  1. Remind the students to save their Choregraphe files before closing the program. 
  2. Pack up the NAO’s, computers and router.
  3. Encourage students to review the students' reference sheet.

 

 

 

REFLECT

Answer the following questions. Be honest. Your teacher will use your answers to help plan future lessons. 

 

What does mirroring mean?

 

What arm motion can I do that NAO cannot do?

 

What did I make NAO do today?






 

After the Lesson
 

  1. Save your Choregraphe files.
  2. Help your teacher pack up the NAO robot computers and router with an extreme care. 
  3. Use the reference sheet to review what you have learned today.