Lesson Modules
Teaching Tips:
This module is an introduction to the concept of multi-tasking. Students can read for themselves.
Multi-Tasking
We do many things simultaneously in our day-to-day life. Chatting while walking, and eating while watching television are common examples. In computer science, this process is known as multi-tasking. A task is something that can be performed independently; multi-tasking is the process of performing many tasks in parallel.
Within each computer (and robot), there is a CPU that handles the processing of tasks. CPU stands for Central Processing Unit, and is where all the computational operations are processed in the computer.
How is multi-tasking done on a CPU? A CPU core can only execute one sequence of instructions at a time. One way to do multi-tasking is to use a multi-core CPU, so that multiple sequences of instructions can be executed concurrently.
But the NAO’s CPU has only a single core. Although only one sequence of program instructions can be executed at a time, the operating system is able to maintain an illusion of true concurrency. The different programs are split into threads. Threads are sequences of code to be executed. The operating system switches which thread is currently executing on the CPU thousands of times per second. This switching is faster than a human’s perception, and provides the illusion that all of the threads are executing simultaneously.
In the figure below, the operating system rapidly switches between three threads. As such, it appears as if all three threads are running in parallel. Notice that the amount of time each thread runs is not constant, and threads do not always run in the same order. The operating system decides when and how to switch between threads.

But we don’t need to worry about the underlying behavior of threads or the operating system on the NAO, since Choregraphe takes cares of this for us.
Teaching Tips:
You can download the code for this module here.
The code is a timeline box with the 4 layers of behavior as shown in the image. You can download the file, open it with Choregraphe and double click on t to show the layers.
Behavior Layers in Choregraphe
Behavior Layers are a feature in Choregraphe similar to threads. Each layer (or behavior) defines a separate thread that will run on the NAO. Some behaviors could be moving an arm, turning the head, saying something, or turning the LEDs on and off.
In the following exercises, we will show how to create behavior layers in Choregraphe to have the NAO do the robot dance.
Teaching Tips:
You can find the code for this module here .
A detailed step by step guide to the module is under CLASS VIEW.
In this lesson, we’ll learn how to use behavior layers on the NAO. Behavior layers allow the NAO to perform multiple tasks on the NAO at the same time. This is known as multi-tasking.
Basic Task: Arms and Head
In this lesson, we’ll learn how to use behavior layers on the NAO. Behavior layers allow the NAO to perform multiple tasks on the NAO at the same time. This is known as multi-tasking. Let’s implement the robot dance, and make the NAO move its arms up and down and shake its head at the same time.
1. In a new Choregraphe project, create a new “Timeline” box.
2. Connect a Motor on box, Stand Up box, an Init Pose box, your new timline box, and a second Init Pose box, as shown below. The robot will stand up, go to its initial position, dance, and return to the initial position. Recall that you can open the Pose Library by clicking View -> Pose library in the top menu bar. 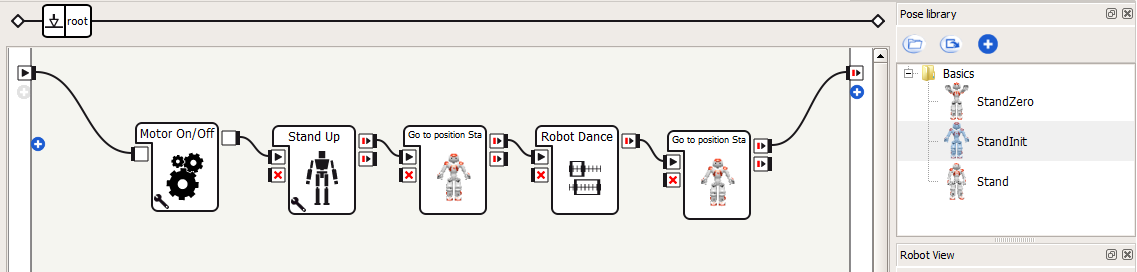
3. Double click on your new timline box to edit it. Beneath the timeline and the word “Motion”, you will see the words “Behavior layers” with a plus sign next to it. Click the plus sign to add a new behavior layer. We will make this layer move the arms up and down.
4. Select the new layer, and add a custom timeline box. Connect it to the initial play arrow, and also connect it to itself. This causes the box to repeat forever.
5. double click on the box and create using the simulated robot arm movements. At this point you need to store the position and make sure the movement stops at 115 frames.
6. Do the same procedure in another behavior layer for the head, creating "yes" and " no" head movements.
7. Play the behavior. The NAO should move its arms and shake its head, doing the robot dance. If the motions appear unstable, try reducing the frame rate.
8. (Optional) Try experimenting with the frequencies of the different layers to find a combination that is visually pleasing.
Teaching Tips:
You can download the code for this module here
The step by step guide for this code is under CLASS VIEW
Intermediate Task: Completing the Robot Dance
In the previous exercise, we finished the basic robot dance. Now we will add in leg motions, flashing lights, and speech.
1. First, add leg motions. As in the previous exercise, add a new behavior layer, Legs, with two keyframes. In one of the keyframes, make the robot squat, and in the second, make it stand up straighter. Be sure to only store angles for the legs in these keyframes
2. Play the entire dance to make sure that the robot doesn’t fall over. If the robot does fall, try slowing down the rate of the squat motion, or make the robot stand up less tall. Changing the frequency of motion of the arm and head may also help. Make a dance that is stable and visually appealing.
3. The beauty of using behavior layers is that you can change the speed of one aspect of the dance, while keeping the rest constant. Try changing the frequency of motion of the arm so that it matches the squats, and make the head bob at a different frequency.
4. We have finished with the dance motions. Add another layer for the NAO to speak. Place an infinitely repeating Say box in the layer, and have the robot say something of your choosing, such as “Nao.” You may also choose to add a Wait box to this layer, if you wish. Click the wrench on the Wait box to set how long the delay should be (in seconds) between saying words. The Wait box in NAO v6 is in programming tab, time folder
5. Now add the final behavior layer, which will control the LEDs. Place a bunch of loops with pairs of LED boxes, one to turn the LEDs on and one to turn them off.
6. Click on the wrenches to set each box’s parameters. Choose an appropriate duration (in seconds), and make the intensity 100% in the first box and 0% in the second box. This will make the lights blink continuously. For the eye LEDs, you can double click on the boxes to select colors.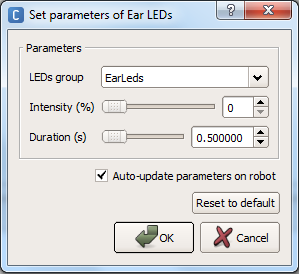
7. (Optional) Add another layer to play music of your choosing.
8. Now play the entire dance. It should include arm, head and leg motions, along with speech and flashing lights.
Teaching Tips:
You can find the code for this module here.
The step by step guide to programming for this module is under CLASS VIEW
The goal of the module is using Python to do something fancier, and have the NAO do part of the robot dance while walking in a circle. To do this, we will have the NAO use the omni-directional walk. We will record the odometry information as it walks to determine when we are finished.
Advanced Task: Walking in Circles
We have finished the robot dance. Now, let’s try doing something fancier, and have the NAO do part of the robot dance while walking in a circle. To do this, we will have the NAO use the omni-directional walk. We will record the odometry information as it walks to determine when we are finished.
1. First, remove the behavior layers for controlling the arms and the legs. The NAO cannot do these motions while walking stably.

2. Next, add a new behavior layer for the walk. Create a new box in this layer, connected to both the start and end arrows. Double click on the box to edit the python code. We will be adding functions into the code, bit by bit. 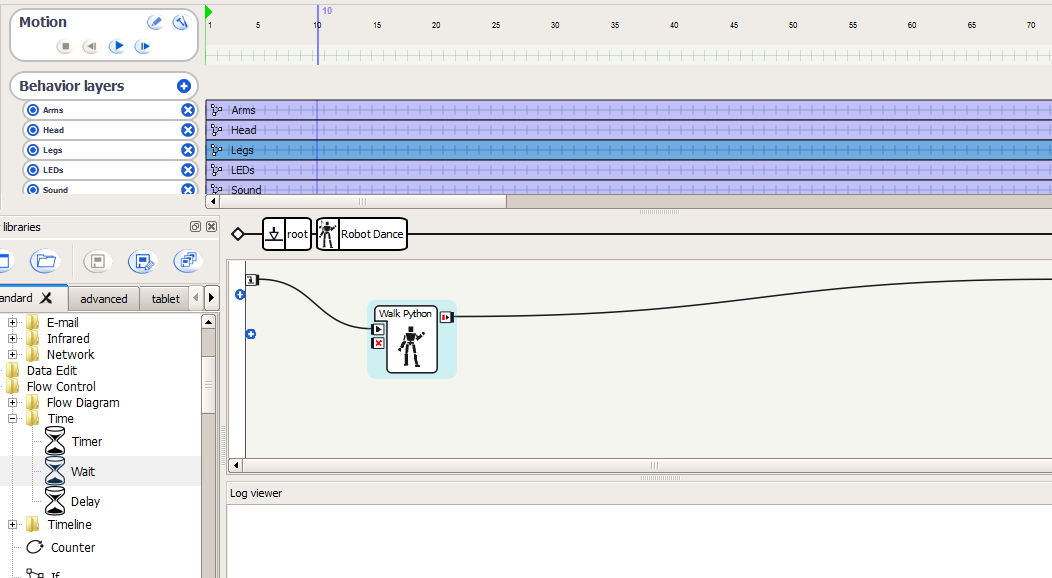
3. Before we begin editing and adding functions to the code, we need to import the relevant libraries. Add the following lines before the class MyClass line. 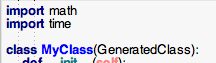
4. The first function we will edit is__init__. 
__init__ is called only once (init stands for initialization), before the behavior starts executing. You have created a proxy to ALMotion in the past within the onInput_onStart function. The main difference here is that the variable name is self.motionProxy instead of just motionProxy. The addition of self. means that motionProxy is now a member variable of the class - it can be accessed in other functions.
5. Next, we will create a new function,simplifyAngle. 
The while structure is a loop, similar to a for loop. However, instead of iterating over some value, it repeats until the condition in the loop evaluates to false. So the first loop will continue subtracting 2pi from theta until it is less than pi . Similarly, the second loop will continue adding 2pi until theta is more than -pi . Thus, simplifyAngle normalizes theta (in radians) to between -pi and pi .
6. We will now create another function, updateTheta. 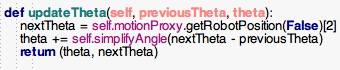
The updateTheta function computes how much we have rotated so far (also known as odometry). ALMotion’s function, getRobotPosition, returns the pose of the robot
(x, y, theta) in global coordinates based on where the NAO first started. Since we are only interested in the amount of rotation, we access the third element in the array (array indices start from 0, so we retrieve element [2]).
Also, we only want the change in position since the Circle box started, not since the robot started, and the second line maintains this information.
Finally, we return the amount of rotation since the Circle box started (theta), and the current global angle of the robot (nextTheta) - that is used for future calculations of updateTheta.
7. Lastly, we will edit the onInput_onStart function - this function is called when the box executes, which we have done in previous exercises. We will use this function to have the NAO walk in a complete circle and then stop walking.
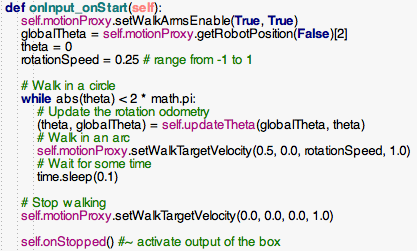
The first line calls setMoveArmsEnabled on ALMotion, which enables the swinging of the arms as the NAO walks. The swinging of the arms helps to keep the NAO balanced.
The next three lines initialize variables. globalTheta stores the global angle of the robot when the box starts executing; theta stores the rotation so far (0 since the robot hasn’t started walking yet); rotationSpeed is a value from -1 to 1 that controls how quickly the robot will rotate.
Thewhile loop continues executing until the odometry for theta exceeds 2pi , meaning that the circle is complete. Inside the loop, setWalkTargetVelocity is called to set the velocity of the NAO’s walk. The first 3 parameters are velocity in the x (forward), y (sideways, to the left), and theta (rotation, counter-clockwise) directions. Since we want the robot to walk in an arc, the walk velocity is set to 0.5 in the forward direction and 0.25 in the rotational direction. This makes the robot walk in an arc, where it walks forward and rotates at the same time.
The time.sleep function puts the thread to sleep, so the CPU can focus on other tasks. Without this line, the robot would execute this loop as fast as possible, but this is unnecessary and a waste of processing time.
Finally, we set the walk velocity back to zero. This stops the robot’s walk once the circle is complete. Otherwise, the function would end but the robot would continue walking.
8. The behavior will currently stop when it reaches the red flag you placed on the timeline previously. Right click on the red flag, and select “Reset end frame.” Now the behavior will end when the robot finishes walking in a circle. 
9. Run the behavior. The robot should walk in a circle and stop.
WARNING: do not hit the red X button to stop the behavior. Otherwise, the robot may continue walking endlessly. If the NAO does walk endlessly, create a new project with a single Walk Toward box, and set the walk velocity in all directions (x, y and theta ) to 0.
10. Measure the odometry error at the end of the behavior. That is, how far does the robot’s final position differ from its initial position?
11. Does the robot walk in a clockwise or counter-clockwise circle? Change the code so that the robot walks in the opposite direction.
12. Measure the radius of the circle the robot walked in. How can you change the radius of the circle that the NAO walks? Make the NAO walk in circles of radii 0.25 m and 1 m.
13. Look again at the simplifyAngle method. This algorithm works, but it is terribly inefficient. What will happen if a very large number is passed to the function? How many times will the loop repeat? In computer science, this algorithm is called O(Ɵ) (“big-O of theta”), meaning that the runtime increases linearly with Ɵ. The simplifyAngle function can be written to be O(1) , meaning the runtime does not depend on Ɵ and the algorithm always runs in constant time. Rewrite the simplifyAngle algorithm to be O(1) . Your new function should not include any loops.
Hint: Use int(number) to truncate (cut off the parts after the decimal) the number to an integer. So, int(1.2) = 1, int(2.0) = 2, and int(1.9999) = 1.
Teaching Tips:
- Modify the robot dance so that the NAO only bobs its head up and down each time you touch the head sensors.
Hint: add a Tactile Head box that links to the Head keyframe in the behavior layer. - Make the NAO walk in a square (building off the earlier exercise) and perform a different combination of speech and/or motion as it traverses each edge of the square.
- Make the NAO walk in a figure eight while doing the robot dance (minus the arms).
Teaching Tips:
Solutions
Basic:
- What does CPU stand for?
Central Processing Unit.
- Explain, at a high level, how a single processor performs multi-tasking.
The operating system executes one thread for a tiny slice of time, and then quickly switches to the next one to provide the illusion of true concurrency.
Intermediate:
- Explain the use for behavior layers.
Behavior layers allow multiple behaviors using different body parts to be executed simultaneously in Choregraphe.
- Why does standing up straighter make the robot more susceptible to falling?
Because the robot’s center of gravity is higher, a smaller tilt will make it leave the stable base region of the feet.
Advanced:
- Why did we need to use the simplifyAngle method when computing the odometry?
To prevent wraparound issues. Let’s say that in one frame, the angle returned for the robot’s position is (pi) - 0.1 , and the next frame the robot rotates 0.2 radians. Then the new angle is -(pi) + 0.1 . Without the simplifyAngle method, we would calculate that in this frame, the robot turned nearly 2(pi) radians as opposed to the actual rotation of 0.2 radians. This makes quite a difference!
- Explain the use of the setWalkTargetVelcoity function.
This sets a velocity - a direction and speed - for the robot to walk in. The velocity has x, y and rotational components. The robot continues to walk at this velocity until a new command is given.
- Why did we need to call time.sleep in the main loop?
Otherwise the main loop will needlessly consume all the computation available, which is wasteful and prevents other important tasks from executing (such as the software making the robot walk).
- Why do we have to set the walk velocity to zero at the end of the loop?
Otherwise the robot won’t stop walking.
- Using only division, multiplication, addition, subtraction, and integer truncation, compute the remainder of x / y in python. (This function, called modulus, is already implemented in python as the % operator. But do not use the % operator.)
x - int(x / y) * y
- Find the big-O runtime cost of the following functions:
c. Finding the correct n-bit key to open a lock by trying every possible key (this is called a brute force attack in computer security).
O(2n)
d. Sorting a list of numbers by finding the lowest number of the entire list, placing it first, finding the next lowest number, placing it second, and so on. This is called selection sort.
O(2n) . There are faster sorting algorithms which are O(n long n).
Questions
Basic:
Intermediate:
Advanced:

